seychellesartprojects.org

Mikä on rajaetu?

Marginal Benefit auttaa organisaatiota määrittämään optimaalisen kulutuksesta saatavan hyödyn ja laskee arvioidun tuotteen / palvelun määrän, jota markkinat vaativat, mikä lisää kustannustehokkuutta yrityksen hoidossa. Lyhyesti sanottuna se auttaa organisaatiota hoitamaan liiketoimintaansa tehokkaammin.

Marginaalietu on asteittainen kasvu kuluttajan hyväksi seurauksena ostetun tuotteen tai palvelun ylimääräisen yksikön lisääntyneestä kulutuksesta. Kuluttajan tyytyväisyys pyrkii laskemaan kulutuksen kasvaessa.

Rajahyötykaava

Marginaalietuuskaava = Kokonaisedun muutos / Kulutettujen yksiköiden määrän muutos

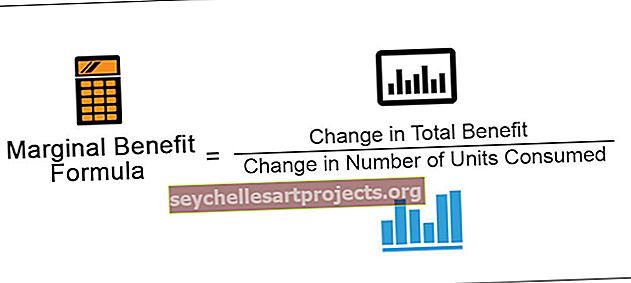
Muutos kokonaiseduissa

Tämä osa käsittää kokonaishyötyjen muutoksen ja saadaan vähentämällä nykyisen kulutuksen kokonaishyöty aiemmasta kulutuksesta. Kehitämme parempaa ymmärrystä seuraavan esimerkin avulla. Oletetaan, että kuluttamalla ensimmäinen banaani, kuluttaja hyötyy 10 yksiköstä, kun taas toinen banaani johtaa kokonaishyötyyn 18. Jotta saavutettaisiin toisen ja ensimmäisen banaanin kokonaisedun muutos, meidän on vähennettävä banaanin kokonaisetu. ensimmäinen banaani toisesta banaanista. Tuloksena on yhteensä 8 (18-10) hyötyä.

Kulutettujen yksiköiden määrän muutos

Tämä osa käsittää kulutettujen yksiköiden määrän muutoksen laskemisen. Se saadaan vähentämällä kuluttavan yksikön määrä aiemmin kulutetusta yksiköstä. Toisen ja ensimmäisen banaanin kulutettujen yksiköiden muutos on 1 (2-1).

Kun molemmat osat lasketaan, rajahyöty saadaan jakamalla kokonaisedun muutos kulutettujen yksiköiden lukumäärän erolla.

Esimerkkejä

Voit ladata tämän Marginal Benefit Formula Excel -mallin täältä - Marginal Benefit Formula Excel -malli

Esimerkki 1

Oletetaan, että kuluttaja, joka Harry ostaa ja kuluttaa jäätelöä, olkoon jäätelöstä saatavan hyödyn mitattuna 50 yksikköä. Harry kuluttaa vielä kolme jäätelöä. 2., 3. ja 4. jäätelön hyöty on 40, 35 ja 25. Laske marginaalin hyöty jäätelön 1. ja 2. sekä 1. ja 3. yksikölle.

Ratkaisu:

Käytä laskelmissa annettuja tietoja

1. ja 2. jäätelön laskeminen voidaan tehdä seuraavasti:

1. ja 2. jäätelö on (50-40) / (2. - 1. yksikkö)

1. ja 2. jäätelön rajaetu = 10

3. ja 1. jäätelö voidaan laskea seuraavasti:

3. ja 1. jäätelön etu on (50-35) / (3. - 1. yksikkö)

3. ja 1. jäätelön etu on -

3. ja 1. jäätelön rajaetu = 7,5

Esimerkki 2

Herra Peter hoitaa teetä. Aikaisemman myyntikokemuksen perusteella hän on arvioinut seuraavien teidensa nauttimisesta saatavan hyödyn: 

Sinun on laskettava marginaalietu jokaisesta myytystä ylimääräisestä yksiköstä.

Ratkaisu:

Marginaalihyöty tee-määrän määrälle = (300-0) / (1-0)

Vastaavasti voimme laskea marginaalisen hyödyn jäljellä olevalle teemäärälle.

Esimerkki 3

Oletetaan, että herra Harry myy jäätelöä hintaan 10 dollaria. Muuttuvat valmistuskustannukset ovat 5 dollaria yksikköä kohti. Tällöin bruttovoitto on 5 dollaria yksikköä kohti. (Kiinteät kustannukset jätetään huomiotta yksinkertaisuuden vuoksi).

Ratkaisu:

Sunnuntaina hän myy 100 yksikköä, mikä johtaa bruttovoittoon 5 dollaria x 100 yksikköä tai 500 dollaria.

Mutta myynnin lisäämiseksi Harry päättää alentaa hintaa 9 dollariin kukin. Tällä hinnalla ansaitset bruttovoiton 4 dollaria yksikköä kohti.

Alennettujen hintojen ansiosta myyntimäärä kasvaa 180 yksikköön. Ensimmäiset 100 kuluttajaa suostuivat maksamaan 10 dollaria, joten he ovat vieläkin onnellisempia maksaa 9 dollaria. Lisäksi 75 muuta asiakasta liittyi ja on valmis maksamaan 9 dollaria. Bruttovoitto on nyt 720.

Laskenta voidaan tehdä seuraavasti:

Rajahyöty on (720 dollaria - 500 dollaria) / (180 yksikköä - 100 yksikköä)

Myyjä voi laskea lopullisen myyntihinnan liiketoimintaansa vaikuttavien eri tekijöiden perusteella.

Osuvuus ja käyttötarkoitukset

• Optimaalisen hyödyn tason perusteella organisaatio voi laatia budjetin tuotettavaa määrää varten.

Tärkeimmät takeaways

• Asiakkaan saamien etuuksien määrän muutos lisäämällä kulutusta yhdellä ylimääräisellä tavara- / palveluyksiköllä on marginaalinen hyöty.
• Se liittyy käänteisesti kulutukseen, ts. Kulutuksen lisääntyessä marginaalietu vähenee.
• Kun tuotanto tai palvelu kasvaa, kustannusten muutos on tuotannon rajakustannus.
• Se auttaa määrittämään vaaditun palvelun tai tuotteen tehokkaimman tason.
• Se auttaa myös saavuttamaan mittakaavaetuja.