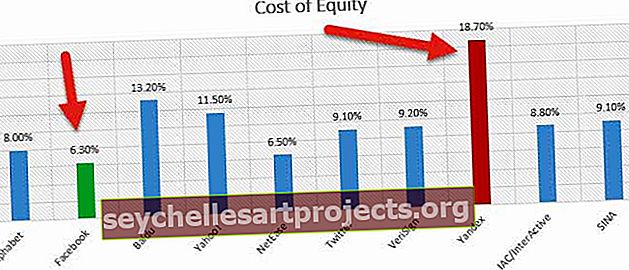
Normaali jakautumiskaava (vaiheittaiset laskelmat)
Normaali jakelukaava
Normaalijakauma on symmetrinen jakauma eli positiiviset arvot ja negatiiviset jakauman arvot voidaan jakaa yhtä suuriin puolikkaisiin, joten keskiarvo, mediaani ja tila ovat samat. Siinä on kaksi häntää, toinen tunnetaan oikealla hännällä ja toinen vasemmalla hännällä.
Laskelman kaava voidaan esittää muodossa
X ~ N (µ, α)
Missä
- N = ei havaintoja
- µ = havaintojen keskiarvo
- α = keskihajonta
Useimmissa tapauksissa havainnot eivät paljasta paljoa raakana. Joten on erittäin tärkeää standardoida havainnot voidakseen verrata sitä. Se tehdään z-pisteiden kaavan avulla. Z-pisteet on laskettava havainnolle.
Z-pistelaskennan yhtälö normaalijakaumalle esitetään seuraavasti:
Z = (X-u) / a
Missä
- Z = havaintojen Z-pisteet
- µ = havaintojen keskiarvo
- α = keskihajonta
Selitys
Jakelu on normaalia, kun se seuraa kellokäyrää. Se tunnetaan kellokäyränä, koska se ottaa kellon muodon. Yksi normaalikäyrän tärkeimmistä ominaisuuksista on, että se on symmetrinen, mikä tarkoittaa, että jakauman positiiviset ja negatiiviset arvot voidaan jakaa yhtä suuriin puolikkaisiin. Toinen erittäin tärkeä ominaisuus muuttujalle on, että havainnot ovat yhden keskihajonnan sisällä keskiarvosta 90% ajasta. Havainnot ovat kaksi standardipoikkeamaa keskimääräisestä 95% ajasta ja kolme standardipoikkeamaa ajan keskiarvosta 99%.
Esimerkkejä
Voit ladata tämän Normal Distribution Formula Excel -mallin täältä - Normal Distribution Formula Excel -malliEsimerkki 1
Opiskelijaluokan painojen keskiarvo on 65 kg ja painon keskiarvo on 5 kg. Jos oletamme, että tuoton jakautuminen on normaalia, tulkitskaamme sitten luokan oppilaiden painoa .
Kun jakauma on normaali, 68% siitä on yhden standardipoikkeaman sisällä, 95% on 2 standardipoikkeaman sisällä ja 99% on 3 standardipoikkeaman sisällä.
Koska
- Painon keskimääräinen tuotto on 65 kg
- Keskihajonta on 3,5 kg

Joten 68% ajasta jakauman arvo on alla olevalla alueella,

- Yläalue = 65 + 3,5 = 68,5
- Alempi alue = 65-3,5 = 61,5
- Kukin häntä (68% / 2) = 34%
Esimerkki 2
Jatketaan samalla esimerkillä. Opiskelijaluokan painojen keskiarvo on 65 kg ja painon normi on 3,5 kg. Jos oletamme, että tuoton jakautuminen on normaalia, tulkitskaamme sitä luokan oppilaiden painon mukaan.
Koska
- Painon keskimääräinen tuotto on 65 kg
- Keskihajonta on 3,5 kg

Joten 95% ajasta jakauman arvo on alla olevalla alueella,

- Yläalue = 65 + (3,5 * 2) = 72
- Alempi alue = 65- (3,5 * 2) = 58
- Kukin häntä (95% / 2) = 47,5%
Esimerkki 3
Jatketaan samalla esimerkillä. Opiskelijaluokan painojen keskiarvo on 65 kg ja painon normi on 3,5 kg. Jos oletamme, että tuoton jakautuminen on normaalia, tulkitskaamme sitä luokan oppilaiden painon mukaan.
Koska
- Painon keskimääräinen tuotto on 65 kg
- Keskihajonta on 3,5 kg


Joten 99% ajasta jakauman arvo on alla olevalla alueella,
- Yläalue = 65+ (3,5 * 3) = 75,5
- Alempi alue = 65- (3,5 * 3) = 54,5
- Kukin häntä (99% / 2) = 49,5%
Osuvuus ja käyttö
Normaalijakauma on erittäin tärkeä tilastollinen käsite, koska suurin osa rahoitusmaailman satunnaismuuttujista seuraa tällaista käyrää. Sillä on tärkeä osa salkkujen rakentamisessa. Rahoituksen lisäksi havaitaan, että monet tosielämän parametrit seuraavat tällaista jakautumista. Kuten esimerkiksi, jos yritämme löytää oppilaiden korkeuden luokassa tai oppilaiden painon luokassa, havainnot jakautuvat normaalisti. Samoin kokeen arvosanat seuraavat samaa jakaumaa. Se auttaa normalisoimaan pisteitä tentissä, jos suurin osa opiskelijoista pisteytti läpäisevien pisteiden alapuolella asettamalla rajan sanomasta, että vain ne, jotka epäonnistui, jotka saivat alle kahden keskihajonnan.