seychellesartprojects.org

Mikä on harmoninen keskiarvo?

Harmoninen keskiarvo on vastavuoroisen aritmeettisen keskiarvon vastavuoroinen, ts. Keskiarvo lasketaan jakamalla annetussa tietojoukossa olevien havaintojen lukumäärä sen tietyn joukon kaikkien havaintojen vastaavuuksien summalla (1 / Xi).

Harmoninen keskimääräinen kaava

Harmoninen keskiarvo = n / ∑ [1 / X _i ]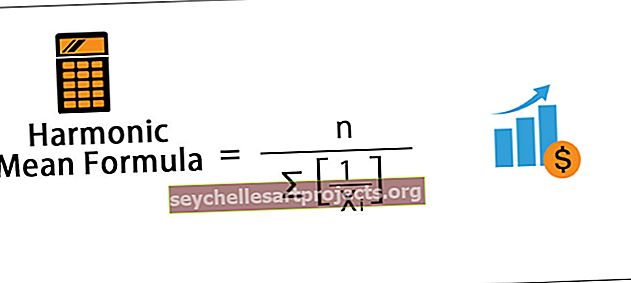

• Voidaan nähdä, että se on normaalin keskiarvon vastavuoroisuus.
• Harmoninen keskiarvo normaalille keskiarvolle on ∑ x / n, joten jos kaava käännetään päinvastaiseksi, siitä tulee n / ∑x ja sitten kaikkien käytetyn nimittäjän arvojen tulisi olla vastavuoroiset, eli osoittajalle se pysyy "n", mutta nimittäjä arvot tai niiden havainnot, joita meidän on käytettävä vastavuoroisiin arvoihin.
• Johdettu arvo olisi aina keskimääräistä pienempi tai sanoa aritmeettinen keskiarvo.

Esimerkkejä

Voit ladata tämän harmonisen keskimääräisen kaavan Excel-mallin täältä - harmonisen keskiarvon kaavan Excel-malli

Esimerkki 1

Harkitse seuraavien numeroiden tietojoukkoa: 10, 2, 4, 7. Edellä esitetyn kaavan avulla sinun on laskettava harmoninen keskiarvo.

Ratkaisu:

Käytä laskennassa seuraavia tietoja.

Harmoninen keskiarvo = n / ∑ [1 / X _i ]

= 4 / (1/10 + 1/2 + 1/4 + 1/7)

= 4 / 0,99

Esimerkki 2

Mr.Vijay on JP Morganin osakeanalyytikko. Hänen johtajansa on pyytänyt häntä määrittämään indeksin P / E-suhde, joka seuraa yhtiön W, Company X ja Company Y osakekursseja. Yritys W ilmoittaa tulot 40 miljoonaa dollaria ja markkina-arvo 2 miljardia dollaria, yritys X raportoi tulot 3 miljardia dollaria ja markkina-arvo 9 miljardia dollaria, ja vaikka yritys Y raportoi tulot 10 miljardia dollaria ja markkina-arvo 40 miljardia dollaria. Laske indeksin P / E-suhteen harmoninen keskiarvo.

Ratkaisu:

Käytä laskennassa seuraavia tietoja

Ensin lasketaan P / E-suhde

P / E-suhde on pääosin (markkina-arvo / voitto).

• (Yritys W) P / E = (2 miljardia dollaria) / (40 miljoonaa dollaria) = 50
• (Yritys X) P / E = (9 miljardia dollaria) / (3 miljardia dollaria) = 3
• (Yritys Y) P / E = (40 miljardia dollaria) / (10 miljardia dollaria) = 4

1 / X-arvon laskeminen

• Yritys W = 1/50 = 0,02
• Yritys X = 1/3 = 0,33
• Yritys Y = 1/4 = 0,25

Laskenta voidaan tehdä seuraavasti,

Harmoninen keskiarvo = n / ∑ [1 / X _i ]

• = 3 / (1/50 + 1/3 + 1/4)
• = 3 / 0,60

Esimerkki 3

Rey, joka asuu Pohjois-Kaliforniassa, on ammattilaisurheilupyöräilijä ja on kiertueella rantaan kotonaan sunnuntai-iltana noin kello 17.00 EST. Hän ajaa urheilupyörällä 50 mph matkan ensimmäisellä puoliskolla ja 70 mph toisella puoliskolla kotoaan rannalle. Mikä on hänen keskinopeutensa?

Ratkaisu:

Käytä laskennassa seuraavia tietoja.

Tässä esimerkissä Rey lähti matkalle tietyllä nopeudella, ja tässä keskiarvo perustuisi etäisyyteen.

Laskenta voidaan tehdä seuraavasti,

Tässä voimme laskea Harmonisen keskiarvon Reyn urheilupyörän keskinopeudelle.

Harmoninen keskiarvo = n / ∑ [1 / X _i ]

• = 2 / (1/50 + 1/70)
• = 2 / 0,03

Reyn urheilupyörän keskinopeus on 58,33.

Käyttö ja osuvuus

Harmonisilla keinoilla, kuten muillakin keskimääräisillä kaavoilla, niillä on myös useita käyttötapoja, ja niitä käytetään pääasiassa rahoitusalalla tiettyjen tietojen, kuten hintakertojen, keskittämiseen. Taloudellisia kerrannaisia, kuten P / E-suhdetta, ei saa laskea keskiarvona käyttäen normaalia keskiarvoa tai aritmeettista keskiarvoa, koska nämä keskiarvot ovat suuntautuneet suurempiin arvoihin. Harmonisia keskiarvoja voidaan edelleen käyttää myös tietyn tyyppisten mallien, kuten Fibonacci-sekvenssien, tunnistamiseen markkinateknikkojen teknisessä analyysissä.

Harmoninen keskiarvo käsittelee myös yksiköiden keskiarvoja, kuten nopeuksia, suhteita tai nopeutta jne. On myös tärkeää huomata, että siihen vaikuttavat tietyn tietojoukon tai tietyn havainnointijoukon ääriarvot.

Harmoninen keskiarvo määritellään jäykästi ja perustuu kaikkiin tietojoukon tai näytteen arvoihin tai kaikkiin havaintoihin, ja se voi olla sopiva matemaattiseen jatkokäsittelyyn. Geometrisen keskiarvon tavoin myöskään harmoniseen keskiarvoon ei vaikuta paljoakaan havaintojen tai näytteenoton vaihtelut. Tämä kiinnittäisi enemmän huomiota pieniin arvoihin tai pieniin havaintoihin, ja tämä on hyödyllistä vain, kun näille pienille arvoille tai pienille havainnoille on annettava suurempi painoarvo.