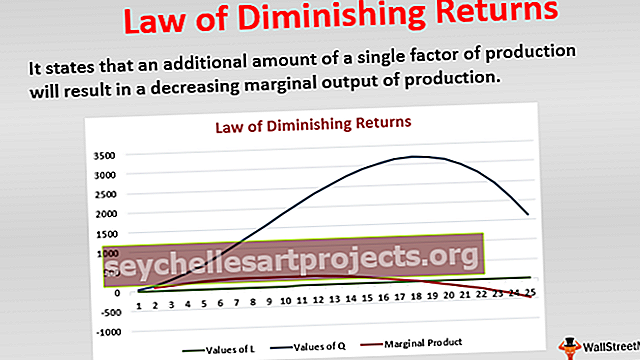
Tuoton vähenemisen laki (määritelmä, esimerkkejä) Kaavion kanssa
Laskevan palautuksen laki Määritelmä
Pienenevän tuoton laki sanoo, että yksittäisen tuotannontekijän lisääminen johtaa tuotannon rajatuotannon vähenemiseen. Laki olettaa muiden tekijöiden olevan vakioita. Tämä tarkoittaa sitä, että jos X tuottaa Y: tä, on kohta, jolloin X: n suurempien määrien lisääminen ei auta Y: n määrien marginaalisessa kasvussa.

Yllä olevassa laskussa laskevien tuottojen laista, kun tekijä X nousee yhdestä yksiköstä 2 yksikköön, Y: n määrä kasvaa. Mutta kun X: n määrät nousevat edelleen P: ksi, tuotanto olettaa laskevan nopeuden Yp: ään saakka. Tämä kuvaa yllä olevaa lakia. Toinen huomattava näkökohta on se, että tulee piste, jolloin X-yksiköiden lisäkasvu vähentää vain Y: n tuotantoa. Siten kasvava panos ei vaikuta vain rajatuotteeseen vaan myös kokonaistuotteeseen. Tätä lakia sovelletaan enimmäkseen tuotantoympäristössä.
Palautusten vähenemisen lain komponentit
Pienentyvän tuoton lain määritelmästä on kolme komponenttia.

- Tuotantokerroin - Mikä tahansa panos, joka tuottaa halutun määrän tuotosta. Tuoton vähenemisen lain osalta otetaan huomioon vain yksi tekijä kerrallaan.
- Rajatuote - Jokaisen lisäpanoksen yhteydessä kokonaistuotteen kasvua kutsutaan rajatuotteeksi. Kaaviossa edellä, Y 2 -Y 1 on marginaalinen tuote.
- Kokonaistuote - Kun panosta käytetään prosessin kautta, tulos tai tulos aggregaattimittauksena on kokonaistuote.
Marginaalisen tuoton vähenemistä koskevan lain oletukset
- Lakia käytetään lähinnä ottamalla huomioon lyhyen aikavälin tuotantoskenaario. Tämä johtuu siitä, että periaate on pitää kaikki muut tuotantotekijät vakioina, lukuun ottamatta sitä, jota käytetään korreloimaan tuotannon kanssa. Tämä ei ole mahdollista pitkällä aikavälillä tuotannossa.
- Panos ja prosessi (t) tulisi pitää riippumattomina teknologisista näkökohdista, koska tekniikalla voi olla oma osansa tuotannon tehokkuuden parantamisessa.
Esimerkkejä marginaalituoton vähenemisen laista
Alla on esimerkkejä laskevan tuoton laista.
Voit ladata tämän Laskun palauttamisen Excel-mallin täältä - Lain pienenevästä palautuksesta Excel-mallinEsimerkki 1
Oletetaan, että tehdas tuottaa tietyn tavaran, jonka antaa seuraava yhtälö:
Q = -L3 + 27L2 + 15L
Missä,
Q on tuotannon määrä
L on panos työvoimana
Kuvaile, sovelletaanko tuoton vähenemisen lakia, jos kyllä, miten?
Ratkaisu:
Tämän lain sovellettavuuden tarkistamiseksi määrittelemme tuotantoyksiköt olettamalla erilaiset työvoiman panosarvot.

Piirrämme Q: n ja L: n arvot kaavioon analyysia varten. Y-akseli edustaa tuotetta (kokonais- ja marginaali). X-akseli edustaa työyksiköitä.

Yllä olevassa laskevan palautuskaavion laissa kaksi pistettä ovat kriittisiä laille:
- Kohta A - rajoittava marginaalituote ja
- Piste B - rajoittava kokonaistuote.
Seuraavat seikat ovat huomionarvoisia:
Voimme jakaa tämän tuotantokaavion kahteen vaiheeseen rajatuotannon suhteen.
- Työvoiman panoksen kasvaessa myös rajatuote kasvaa ennen useita työntekijöitä, L = 9. Tämä on tuoton kasvuvaihe.
- Yhdennentoista työvoimayksikön tuottama rajatuote on alle kymmenesosa. Tämä aloittaa tuoton vähenemisen vaiheen.
Kokonaistuote eli Q: n määrä ei vähene ennen kuin 20. työntekijä otetaan palvelukseen. Selvästi rajatuote siirtyy täältä negatiivisten tuottojen vaiheeseen.
Tehdas voi työllistää 9 työntekijää pitääkseen marginaalituotteen kasvussa. Se voi kuitenkin lisätä jopa 19 työntekijää ennen kuin huomaa kokonaistuotteen laskun.
Esimerkki 2
Viljelijä omistaa pienen vehnäpellon. Hän alkaa viljellä maata yhden työntekijän kanssa. Hän lisää vähitellen kuuteen työntekijään vain huomatakseen, että hänen vehnäntuotantonsa ei ole kasvanut suhteellisesti. Auta viljelijää analysoimaan optimaalinen tarvittava työvoima.

Ratkaisu:
Yksinkertaisesti tarkastelemalla vehnäntuotantoa käytettyyn työvoimaan nähden voimme sanoa, että rajatuotanto pienenee jokaisen lisätyön myötä. Jos päätämme rajatuotteen ja esitämme sen viljelijälle, se näyttää tältä:

Tämä osoittaa, että rajatuote kasvaa ennen kuin neljännen työntekijän palvelut otetaan käyttöön. Sen jälkeen rajatuote laskee.
Siksi maanviljelijän tulisi optimoida vehnäntuotantonsa kolmen peltomiehen kanssa.
Toisaalta hän voi maksimoida kokonaistuotteensa jatkamalla työntekijöiden lisäämistä. Mutta tämä aiheuttaa pienemmän marginaalituotannon kustannukset.
Nämä kaksi esimerkkiä hyvältä vaiheelta, josta voimme tarkastella ”vähenevän tuoton lain” etuja ja rajoituksia.
Palautusten vähenemisen lain edut
- Pienentyvän tuoton laki auttaa johtoa maksimoimaan työvoiman (kuten yllä olevat esimerkit 1 ja 2) ja muut tuotantotekijät optimaaliselle tasolle.
- Tämä teoria auttaa myös lisäämään tuotannon tehokkuutta minimoimalla tuotantokustannukset, mikä käy ilmi vehnänviljelijän tapauksesta.
Tuoton vähenemisen lain rajoitukset
- Vaikka tämä laki on hyödyllinen tuotantotoiminnassa, sitä ei voida soveltaa kaikissa tuotantomuodoissa. Rajoitus syntyy, kun tuotantotekijät ovat vähemmän luonnollisia ja siksi yleinen käyttö on vaikeaa. Enimmäkseen tätä lakia voidaan soveltaa maatalouden skenaarioissa.
- Lain mukaan oletetaan, että yhden tuotantotekijän kaikkien yksiköiden on oltava samat. Tämä ei kuitenkaan yleensä ole käytännöllistä ja siitä tulee este sovelluksessa. Yllä olevissa esimerkeissämme työvoimasta tulee erityinen panos, muut tekijät pysyvät vakiona.
Johtopäätös
Pienentyvän tuoton laki on hyödyllinen käsite tuotantoteoriassa. Laki voidaan luokitella kolmeen vaiheeseen - tuottojen kasvaminen, tuottojen väheneminen ja negatiiviset tuotot. Tuotantoteollisuus ja erityisesti maatalousala pitää tätä lakia valtavasti soveltavana. Tuottajat asettavat kyseenalaiseksi, mihin rajatuotteen kaavioon tulisi toimia, koska ensimmäinen vaihe kuvaa alikäytettyä kapasiteettia ja kolmas vaihe on liikaa käytettyjä panoksia. Optimaalisen kapasiteetin saavuttaminen on siis tämän lain perusta.