Vakiopoikkeaman kaava Vaiheittainen laskenta
Mikä on standardipoikkeaman kaava?
Vakiopoikkeama (SD) on suosittu tilastointityökalu, jota edustaa kreikkalainen kirjain σ ja jota käytetään mittaamaan joukko tietoarvojen vaihteluita tai hajonta suhteessa sen keskiarvoon (keskiarvo), tulkitsemaan siten tiedot. Jos se on pienempi, datapisteet ovat lähellä keskiarvoa, mikä osoittaa luotettavuutta. Mutta jos se on suurempi, datapisteet leviävät kaukana keskiarvosta.
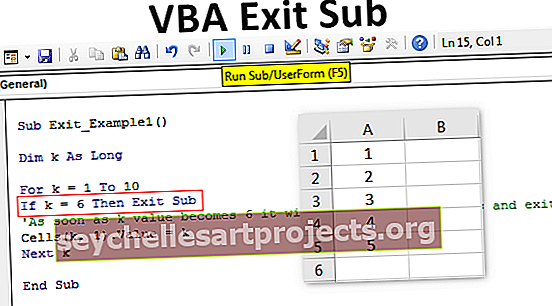
Keskihajonnan kaava on annettu alla


Missä:
- xi = kunkin datapisteen arvo
- x̄ = Keskiarvo
- N = datapisteiden lukumäärä
- Keskihajontaa käytetään ja harjoitellaan yleisimmin salkunhoitopalveluissa, ja rahastonhoitajat käyttävät usein tätä perusmenetelmää laskeakseen ja perustellakseen tuotonsa vaihtelua tietyssä salkussa.
- Salkun korkea keskihajonta tarkoittaa, että tietyssä osakesalkussa on suuri varianssi tietyssä osakemäärässä, kun taas toisaalta matala keskihajonta merkitsee vähemmän osakekohtaista vaihtelua keskenään.
- Riskin välttävä sijoittaja on halukas ottamaan lisäriskin vain, jos hänelle kompensoidaan yhtä suuri tai suurempi tuotto kyseisen riskin ottamiseksi.
- Riskialttiimpi sijoittaja ei välttämättä ole tyytyväinen keskihajontaansa ja haluaisi lisätä turvallisempia sijoituksia, kuten valtion joukkolainoja tai suurikapasiteettisia osakkeita salkkuunsa tai sijoitusrahastoihin, jotta hajautettaisiin salkun ja sen riskit keskihajonta ja varianssi.
- Varianssi ja siihen läheisesti liittyvä keskihajonta ovat mittoja jakauman jakautumisesta. Toisin sanoen, ne ovat vaihtelevuuden mittareita.
Vaiheet keskihajonnan laskemiseksi
- Vaihe 1: Ensinnäkin havaintojen keskiarvo lasketaan samalla tavalla kuin keskiarvo, joka lisää kaikki tietojoukossa käytettävissä olevat datapisteet ja jakamalla sen havaintojen määrällä.
- Vaihe 2: Sitten jokaisen datapisteen varianssi mitataan keskiarvolla, joka voi olla positiivinen tai negatiivinen luku, sitten arvo neliöidään ja tulos vähennetään yhdellä.
- Vaihe 3: Vaiheesta 2 laskettu varianssin neliö otetaan sitten keskihajonnan laskemiseksi.
Esimerkkejä
Voit ladata tämän standardipoikkeaman kaavan Excel-mallin täältä - Standard Deviation Formula Excel -malliEsimerkki 1
Datapisteille annetaan 1,2 ja 3. Mikä on annetun tietojoukon keskihajonta?
Ratkaisu:
Käytä seuraavia tietoja keskihajonnan laskemiseen

Varianssin laskeminen on siis -

Varianssi = 0,67
Keskihajonnan laskeminen on -

Keskihajonta = 0,82
Esimerkki 2
Etsi keskihajonta 4,9,11,12,17,5,8,12,14.
Ratkaisu:
Käytä seuraavia tietoja keskihajonnan laskemiseen

Keskiarvon laskeminen on -

Etsi ensin datapisteen 4 + 9 + 11 + 12 + 17 + 5 + 8 + 12 + 14/9 keskiarvo
Keskiarvo = 10,22
Varianssin laskeminen on siis -

Varianssi on -

Varianssi = 15,51
Keskihajonnan laskeminen on -

Keskihajonta = 3,94
Varianssi = Keskihajonnan neliöjuuri
Esimerkki 3
Käytä seuraavia tietoja keskihajonnan laskemiseen

Varianssin laskeminen on siis -

Varianssi = 132,20
Keskihajonnan laskeminen on -

Keskihajonta = 11,50
Salkunhoitajat käyttävät usein tällaista laskutoimitusta laskeakseen salkun riskin ja tuoton.
Osuvuus ja käyttötarkoitukset
- Keskihajonta on hyödyllinen, kun analysoidaan salkun kokonaisriskiä ja palautetaan matriisi, ja koska se on historiallisesti hyödyllistä, sitä käytetään laajalti teollisuudessa. Salkun keskihajonta voi vaikuttaa salkun osakkeiden korrelaatioon ja painoon. .
- Koska salkun kahden omaisuusluokan korrelaatio vähentää salkun riskiä, yleensä se pienenee, ei kuitenkaan ole välttämätöntä koko ajan, että yhtä painotettu salkku tarjoaa vähiten riskiä maailmankaikkeudessa.
- Korkea keskihajonta voi olla volatiliteetin mitta, mutta se ei välttämättä tarkoita, että tällainen rahasto on huonompi kuin alhaisen keskihajonnan omaava. Jos ensimmäinen rahasto on paljon korkeampi kuin toinen, poikkeamalla ei ole merkitystä.
- Vakiopoikkeamaa käytetään myös tilastoissa, ja professorit opettavat sitä laajalti maailman eri korkeakoulujen keskuudessa, mutta standardipoikkeaman kaava muuttuu, kun sitä käytetään otoksen poikkeaman laskemiseen.
- SD: n yhtälö näytteessä = vain nimittäjä pienennetään 1: llä