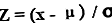seychellesartprojects.org

Kaava Z-pistemäärän laskemiseksi

Raakatietojen Z-pistemäärä viittaa pisteeseen, joka syntyy mittaamalla kuinka monta populaatiokeskiarvon ylä- tai alapuolella olevaa keskihajontaa on, mikä auttaa tarkasteltavan hypoteesin testaamisessa. Toisin sanoen datapisteen etäisyys populaation keskiarvosta ilmaistaan ​​keskihajonnan kerrannaisena.

• Z-pisteet vaihtelevat välillä -3 kertaa keskihajonta (normaalijakauman vasemmassa reunassa) +3 kertaa standardipoikkeama (normaalijakauman oikeassa reunassa).
• Z-pisteiden keskiarvo on 0 ja keskihajonta 1.

Datapisteen z-pistemäärän yhtälö lasketaan vähentämällä populaation keskiarvo datapisteestä (kutsutaan x: ksi ) ja sitten tulos jaetaan populaation keskihajonnalla. Matemaattisesti se on esitetty

Z Pisteet = (x - μ) / ơ

missä

• x = Datapiste
• μ = keskiarvo
• ơ = Keskihajonta

Z-pistemäärän laskeminen (askel askeleelta)

Datapisteen z-pisteen yhtälö voidaan johtaa käyttämällä seuraavia vaiheita:

• Vaihe 1: Ensinnäkin, määrätä keskiarvo Tietueen tietojen perusteella pistettä tai huomautukset, jotka on merkitty x _i , kun koko datapisteiden datasarja on merkitty N.

• Vaihe 2: Määritä seuraavaksi populaation keskihajonta populaation keskiarvon μ, datapisteiden x _i ja populaation N datapisteiden määrän perusteella.

• Vaihe 3: Lopuksi z-pisteet johdetaan vähentämällä keskiarvo datapisteestä ja tulos jaetaan sitten keskihajonnalla, kuten alla on esitetty.

  

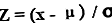
Esimerkkejä

Voit ladata tämän Z Score Formula Excel -mallin täältä - Z Score Formula Excel -malli

Esimerkki 1

Otetaanpa esimerkki 50 opiskelijan luokasta, jotka ovat kirjoittaneet luonnetestin viime viikolla. Tänään on tulospäivä ja luokanopettaja kertoi, että John teki testissä 93, kun taas luokan keskiarvo oli 68. Määritä Johnin testimerkin z-pisteet, jos keskihajonta on 13.

Ratkaisu:

Koska

• Johnin testitulos, x = 93
• Keskiarvo, μ = 68
• Keskihajonta, ơ = 13

Siksi z-pisteet Johnin testipisteille voidaan laskea käyttämällä yllä olevaa kaavaa,

Z = (93-68) / 13

Z-pisteet ovat -

Z-pisteet = 1,92

Siksi Johnin Ztest-pistemäärä on 1,92 keskihajonta luokan keskiarvoa korkeampi, mikä tarkoittaa, että 97,26% luokassa (49 opiskelijaa) teki vähemmän kuin John.

Esimerkki 2

Otetaan toinen yksityiskohtainen esimerkki 30 oppilasta (koska z-testi ei sovellu alle 30 datapisteeseen), jotka ilmestyivät luokkatestiin. Määritä neljännen opiskelijan z-testitulos opiskelijoiden 100 - 55, 67, 84, 65, 59, 68, 77, 95, 88, 78, 53, 81, 73, 66 pisteiden perusteella 65, 52, 54, 83, 86, 94, 85, 72, 62, 64, 74, 82, 58, 57, 51, 91.

Ratkaisu:

Koska

• x = 65,
• 4. opiskelija teki = 65,
• Datapisteiden lukumäärä, N = 30.

Keskiarvo = (55 + 67 + 84 + 65 + 59 + 68 + 77 + 95 + 88 + 78 + 53 + 81 + 73 + 66 + 65 + 52 + 54 + 83 + 86 + 94 + 85 + 72 + 62 + 64 + 74 + 82 + 58 + 57 + 51 + 91) / 30

Keskiarvo = 71.30

Nyt keskihajonta voidaan laskea käyttämällä alla olevaa kaavaa,

ơ = 13,44

Siksi 4. opiskelijan Z-pisteet voidaan laskea käyttämällä yllä olevaa kaavaa,

Z = (x - x) / s

• Z = (65-30) / 13,44
• Z = -0,47

Siksi 4. opiskelijan pisteet ovat 0,47 keskihajonta alle luokan keskimääräisen pistemäärän, mikä tarkoittaa, että 31,92% luokasta (10 opiskelijaa) teki vähemmän kuin 4. opiskelija z-pistetaulukon mukaan.

Z-pisteet Excelissä (Excel-mallilla)

Otetaan nyt esimerkissä 2 mainittu tapaus havainnollistamaan z-pisteen käsitettä alla olevassa Excel-mallissa.

Alla on annettu tietoja Z-pistemäärän laskemiseksi

Voit tarkastella alla olevaa Excel-taulukkoa saadaksesi yksityiskohtaisen laskelman Z Score Formula Test Statistics -tuloksista.

Osuvuus ja käyttötarkoitukset

Hypoteesitestauksen näkökulmasta z-pisteet on erittäin tärkeä käsite ymmärrettäväksi, koska sitä käytetään testaamaan, kuuluuko testitilasto hyväksyttävälle arvoalueelle vai ei. Z-pistettä käytetään myös tietojen standardointiin ennen analyysiä, pisteiden todennäköisyyden laskemiseen tai kahden tai useamman datapisteen vertailuun, jotka ovat peräisin erilaisista normaalijakaumista. Z-pistemääriä voidaan käyttää monipuolisesti eri kentissä, jos niitä käytetään oikein.