Salkun varianssikaava (esimerkki) | Kuinka salkun vaihtelu lasketaan?
Mikä on salkun vaihtelu?
Termi "salkun varianssi" viittaa nykyaikaisen sijoitusteorian tilastolliseen arvoon, joka auttaa mittaamaan salkun keskimääräisen tuoton hajontaa sen keskiarvosta. Lyhyesti sanottuna se määrittää salkun kokonaisriskin. Se voidaan johtaa yksilöllisen varianssin ja keskinäisen kovarianssin painotetun keskiarvon perusteella.
Salkun varianssikaava
Matemaattisesti kahdesta omaisuuserästä koostuva salkun varianssikaava on esitetty
Salkun varianssikaava = w 1 2 * ơ 1 2 + w 2 2 * ơ 2 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2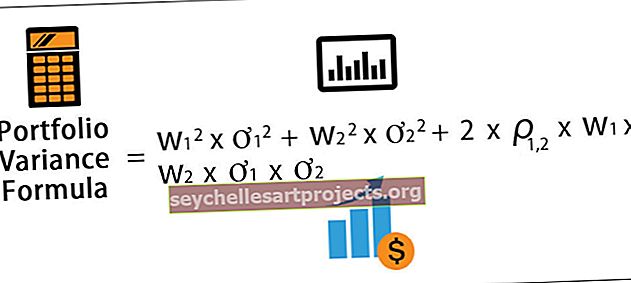
missä,
- w i = omaisuuden i salkun paino
- ơ i 2 = Omaisuuden i yksilöllinen varianssi
- ρ i, j = Omaisuuden i ja omaisuuden j välinen korrelaatio
Jälleen varianssi voidaan laajentaa edelleen salkkuun, jossa on enemmän ei. esimerkiksi kolmen omaisuuden salkku voidaan esittää
Salkun varianssikaava = w 1 2 * ơ 1 2 + w 2 2 * ơ 2 2 + w 3 2 * ơ 3 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2 + 2 * ρ 2,3 * w 2 * w 3 * ơ 2 * ơ 3 + 2 * ρ 3,1 * w 3 * w 1 * ơ 3* ơ 1
Selitys salkun varianssikaavasta
Tietyn salkun salkun varianssikaava voidaan johtaa käyttämällä seuraavia vaiheita:
Vaihe 1: Määritä ensin kunkin omaisuuden paino koko salkusta ja se lasketaan jakamalla omaisuuden arvo salkun kokonaisarvolla. Paino nnen hyödykkeen on merkitty w i .
Vaihe 2: Määritä seuraavaksi kunkin omaisuuden keskihajonta ja se lasketaan kunkin omaisuuden keskimääräisen ja todellisen tuoton perusteella. I: n omaisuuserän keskihajontaa merkitään ơ i: llä . Keskihajonnan neliö on varianssi eli ơ i 2.
Vaihe 3: Määritä seuraavaksi omaisuuserien välinen korrelaatio, ja se kuvaa periaatteessa kunkin omaisuuden liikkeen suhteessa toiseen omaisuuteen. Korrelaatio on merkitty ρ: llä.
Vaihe 4: Lopuksi kahden omaisuuden salkun varianssikaava johdetaan yksilöllisen varianssin ja keskinäisen kovarianssin painotetun keskiarvon perusteella, kuten alla on esitetty.
Salkun varianssikaava = w 1 * ơ 1 2 + w 2 * ơ 2 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2
Esimerkki salkun varianssikaavasta (Excel-mallin kanssa)
Voit ladata tämän Portfolio Variance Formula Excel -mallin täältä - Portfolio Variance Formula Excel -malli
Otetaan esimerkki salkusta, joka koostuu kahdesta osakkeesta. A-osakkeen arvo on 60 000 dollaria ja sen keskihajonta on 15%, kun taas osakkeen B arvo on 90 000 dollaria ja sen keskihajonta on 10%. Kahden osakkeen välillä on korrelaatio 0,85. Määritä varianssi.
Koska
- Varaston A keskihajonta, ơ A = 15%
- Varaston B keskihajonta, ơ B = 10%
Korrelaatio, ρ A, B = 0,85
Alla on tiedot kahden osakkeen salkun varianssin laskemiseksi.

A-osakkeen paino, w A = 60 000 dollaria / (60 000 dollaria + 90 000 dollaria) * 100%

A-osakkeen paino = 40% tai 0,40
B-osakkeen paino, w B = 90 000 dollaria / (60000 dollaria + 90 000 dollaria) * 100%

Osakkeen B paino = 60% tai 0,60
Siksi salkun varianssilaskenta on seuraava,

Varianssi = w A 2 * ơ A 2 + w B 2 * ơ B 2 + 2 * ρ A, B * w A * w B * ơ A * ơ B
= 0,4 ^ 2 * (0,15) 2 + 0,6 ^ 2 * (0,10) 2 + 2 * 0,85 * 0,4 * 0,6 * 0,15 * 0,10

Siksi varianssi on 1,33%.
Osuvuus ja käyttö
Yksi salkun muuttujan silmiinpistävimmistä piirteistä on se, että sen arvo johdetaan kunkin omaisuuserän kovarianssilla oikaistujen yksittäisten varianssien painotetun keskiarvon perusteella. Tämä osoittaa, että kokonaisvarianssi on pienempi kuin salkun kunkin osakkeen yksittäisten varianssien yksinkertainen painotettu keskiarvo. On huomattava, että salkun, jonka arvopapereilla on pienempi korrelaatio keskenään, salkun vaihtelu on pienempi.
Salkun varianssikaavan ymmärtäminen on myös tärkeää, koska sitä voidaan soveltaa Modern Portfolio Theory -sovellukseen, joka perustuu perusolettamukseen, jonka mukaan normaalit sijoittajat aikovat maksimoida tuottonsa samalla kun minimoidaan riski, kuten varianssi. Sijoittaja tavoittelee yleensä niin sanottua tehokasta rajaa, ja se on matalin riski- tai volatiliteettitaso, jolla sijoittaja voi saavuttaa tavoitetuotonsa. Useimmiten sijoittajat sijoittavat korreloimattomiin omaisuuseriin pienentääkseen riskiä Modern Portfolio Theoryn mukaisesti.
On tapauksia, joissa omaisuuserät, jotka saattavat olla erikseen riskialttiita, voivat lopulta pienentää salkun vaihtelua, koska tällainen sijoitus todennäköisesti nousee muiden sijoitusten pudotessa. Sellaisena tämä vähentynyt korrelaatio voi auttaa vähentämään hypoteettisen salkun varianssia. Yleensä salkun riskitaso mitataan käyttämällä standardipoikkeamaa, joka lasketaan varianssin neliöjuurena. Varianssin odotetaan pysyvän suurena, kun datapisteet ovat kaukana keskiarvosta, mikä johtaa lopulta myös salkun kokonaisriskitasoon.