seychellesartprojects.org

Tilastoissa meillä on termi, jota kutsutaan lognormaalijakaumaksi, joka lasketaan selvittämään muuttujan jakauma, jonka logaritmi on normaalisti jakautunut. Alkuperäinen kaava on hyvin monimutkainen kaava sen laskemiseksi, mutta Excelissä meillä on sisäänrakennettu toiminto lognormalin laskemiseksi. Lognorm.Dist-toiminto.

Mikä on Lognormal Distribution Excelissä

Lognormaali jakauma palauttaa satunnaismuuttujan jatkuvan tilastollisen jakauman, joka on normaalisti hajautettu logaritmi. Seuraavassa on Excelissä käytettävät lognormaalien toimintojen tyypit: -

LOGNORM.DIST-kaava

Jakautumistoiminnon syntaksiksi määritetään Excelissä LOGNORM.DIST (x, keskiarvo, standardi_ Dev, kumulatiivinen), joka palauttaa x: n lognormaalin jakauman annetuilla parametreilla luonnollisen logaritmin Ln (x) keskiarvolle ja keskihajonnalle. Yllä oleva toiminto vaatii seuraavat parametrit tai argumentit: -

• x: - vaadittu arvon x arvo, jonka lognormaali jakauma on palautettava.
• keskiarvo: - Ln (x): n keskiarvo
• standard_dev: - Ln (x): n keskihajonta
• kumulatiivinen: - Jos kumulatiivinen on TOSI, funktio palauttaa kumulatiivisen jakauman, muuten FALSE antaa todennäköisyystiheyden.

Kumulatiivisen jakauman funktio (CDF) on todennäköisyysmuuttuja, jonka arvo on pienempi kuin x. Jatkuvan satunnaismuuttujan todennäköisyystiheysfunktio (PDF) selittää satunnaismuuttujan x suhteellisen todennäköisyyden ottaa tietty arvo.

Myös LOGNORM.DIST on yleensä hyödyllinen osakekurssien analysoinnissa, koska normaalijakaumaa ei voida käyttää osakkeiden hinnan laskemiseen. Toimintoa voidaan käyttää myös Black Scholes -mallin optiohinnoittelun laskemiseen.

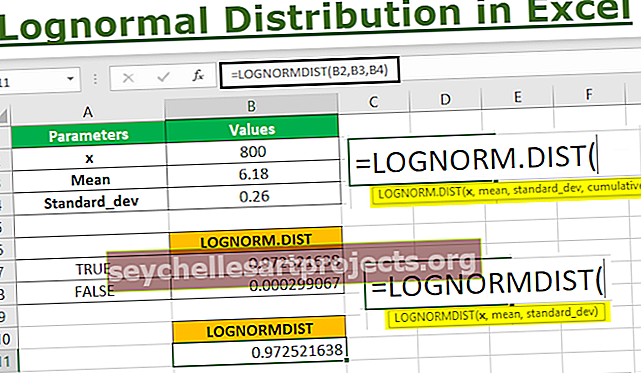
Lognormal Distribution Excel -parametrien laskeminen

Käytään läpi joitakin esimerkkejä Excelissä käytetystä lognormaalijakaumasta.

Voit ladata tämän Lognormal Distribution Excel -mallin täältä - Lognormal Distribution Excel -malli

Harkitse pörssiyhtiöiden osakekurssin alapuolella saadaksesi Excelin keskiarvon ja keskihajonnan.

Vaihe 1: - Laske nyt vastaavien osakekurssien luonnollisen logaritmin arvot.

Kuten yllä olevista tiedoista voidaan nähdä, = LN (luku) palauttaa annetun luvun luonnollisen logaritmin arvon.

Vaihe 2: - Laske seuraavaksi luonnollisten logaritmien numeroiden neliöarvot, sama näkyy alla olevassa taulukossa.

Vaihe 3: - Tarvitsemme nyt myös osakekurssin luonnollisen logaritmin summan ja neliöllisen luonnollisen logaritmin arvojen summan keskihajonnan laskemiseksi.

Vaihe 4: - Laske seuraavaksi osakekurssin luonnollisen logaritmin keskiarvo.

Keskiarvo, µ = (5,97 + 5,99 + 6,21 + 6,54) / 4

Tai µ = 6,18

Vaihe 5: - Keskihajonnan laskeminen voidaan tehdä manuaalisesti ja käyttämällä suoraa excel-kaavaa.

Alla on taulukko osakekurssin keskiarvo- ja keskihajonta-arvoista.

Keskihajonta lasketaan käyttämällä = STDEV.S (Luonnollisen logaritmin sarakkeen alue ln (varastohinta)).

Edellä mainittuja keskiarvon ja keskihajonnan parametreja voidaan kuitenkin käyttää minkä tahansa annetun arvon 'X' tai osakekurssin excel lognormaalin jakauman laskemiseen. Saman selitys on esitetty alla.

Vaihe 1: - Harkitse alla olevaa taulukkoa ymmärtääksesi LOGNORM.DIST-toiminnon

Yllä olevassa taulukossa esitetään parametriarvot, joita tarvitaan laskemaan x: n excel-log-normaalijakauma, joka on 10.

Vaihe 2: - Lisäämme nyt arvot kaavafunktioon tuloksen saavuttamiseksi valitsemalla argumentit B2, B3, B4, ja kumulatiivisella parametrilla on vaihtoehdot TOSI ja EPÄTOSI.

LOGNORM.DIST (x, keskiarvo, vakioviive, kumulatiivinen)

Kuten yllä olevassa kuvakaappauksessa näkyy, kirjoita ensin TOSI-vaihtoehto kumulatiivisen jakelutoiminnon saamiseksi.

Siten saavutetaan arvo, joka on esitetty solussa C19 kumulatiivisen jakautumisen funktiolle (CDF).

Vaihe 3: - Laske nyt lognormaali jakauma Excelissä todennäköisyystiheysfunktiolle (PDF) valitsemalla sama argumentti B2, B3, B4 ja FALSE kumulatiivisessa parametrissa.

Kuten yllä olevasta kuvasta nähdään, saavutetaan tulos solussa C20 todennäköisyystiheysfunktiolle (PDF).

Vaihe 4: - Kuten yllä olevasta toiminnosta näkyy, LOGNORM.DIST on yhteensopiva vuoden 2010 Excel-version ja sitä uudempien versioiden kanssa. Voimme kuitenkin käyttää myös LOGNORMDIST-ohjelmaa, joka käyttää samoja parametreja kuin uusimmat versiot. Kun otetaan huomioon samat parametriarvot, täytetään LOGNORMDIST-funktio alla olevan kuvan mukaisesti.

Kuten voidaan nähdä, arvosta saatiin sama luku kuin LOGNORM.DIST-parametrille TRUE kumulatiivisessa argumentissa.

Muistettavaa Excelin normaalista jakelusta

1. Jos jokin parametri tai argumentti ei ole numeerinen, lognormaali jakauma on excel, funktio palauttaa #ARVO! virheviesti.
2. Jos argumentit x on pienempi ja yhtä suuri kuin 0 tai jos keskihajonta on pienempi ja yhtä suuri kuin 0, funktio palauttaisi #NUM! virheviesti.
3. Vastaava lauseke LOGNORM.DIST-arvon laskemiseksi on LOGNORM.DIST (x, keskiarvo, standardi-dev) = NORM.S.DIST ((ln (x) -merkki) / standardi-dev)
4. Tämä toiminto on yhteensopiva versiolle 2010 ja sitä uudemmille, versioissa 2007 ja aikaisemmissa on käytettävä LOGNORMDIST (x, keskiarvo, vakio_haja), joka palauttaa x: n kumulatiivisen lognormaalijakauman, jossa ln (x) jaetaan normaalisti parametrien / argumenttien keskiarvo ja standard_dev.