P-arvon kaava | Vaiheittaiset esimerkit P-arvon laskemiseksi
Mikä on P-arvon kaava?
P on tilastollinen mitta, joka auttaa tutkijoita selvittämään, onko heidän hypoteesinsa oikea. Se auttaa määrittämään tulosten merkityksen. Nollahypoteesi on oletusasento, jonka mukaan kahden mitatun ilmiön välillä ei ole yhteyttä. Sitä merkitään H 0. Vaihtoehtoinen hypoteesi on se, jonka uskot, jos nollahypoteesi todetaan epätosi. Sen symboli on H 1 tai H a.
P-arvo excelissä on luku välillä 0 ja 1. P-arvon laskemisessa on taulukoita, taulukkolaskentaohjelmia ja tilasto-ohjelmistoja. Merkitsevyystaso (α) on ennalta määritelty kynnys, jonka tutkija on asettanut. Se on yleensä 0,05. Hyvin pieni p-arvo, joka on pienempi kuin merkitsevyystaso, osoittaa, että hylkäät nullhypoteesin. P-arvo, joka on suurempi kuin merkitsevyystaso, osoittaa, että emme hylkää nollahypoteesia.
P-arvon kaavan selitys
Kaava p-arvon laskemiseksi voidaan johtaa käyttämällä seuraavia vaiheita:
P-arvon laskeminen Z-tilastosta
Vaihe 1: Meidän on selvitettävä testitilasto z

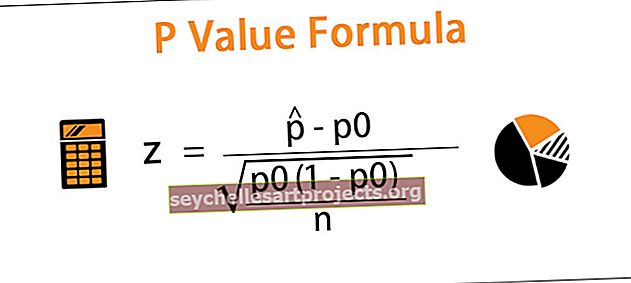
Missä
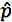 on näytteen osuus
on näytteen osuus- p0 on oletettu populaatioosuus nollahypoteesissa
- n on näytekoko
Vaihe 2: Meidän on löydettävä vastaava p-arvo saadusta z-arvosta. Tätä tarkoitusta varten meidän on tarkasteltava z-taulukkoa.

Lähde: www.dummies.com
Etsitään esimerkiksi p: n arvo, joka vastaa z ≥ 2,81. Koska normaalijakauma on symmetrinen, z: n negatiiviset arvot ovat yhtä suuret kuin sen positiiviset arvot. 2,81 on summa 2,80 ja 0,01. Katso z-sarakkeesta 2,8 ja vastaava arvo 0,01. Saamme p = 0,0025.
Esimerkkejä P-arvon kaavasta (Excel-mallin kanssa)
Katsotaanpa joitain yksinkertaisia ja edistyneitä esimerkkejä P-arvon yhtälöstä sen ymmärtämiseksi paremmin.
Voit ladata tämän P Value Formula Excel -mallin täältä - P Value Formula Excel -malli
Esimerkki 1
a) P-arvo on 0,3015. Jos merkitsevyystaso on 5%, selvitä, voimmeko hylätä nullhypoteesin.
b) P-arvo on 0,0129. Jos merkitsevyystaso on 5%, selvitä, voimmeko hylätä nullhypoteesin.
Ratkaisu:
Käytä seuraavia tietoja P-arvon laskemiseen.

P-arvo on -

a) Koska p-arvo 0,3015 on suurempi kuin merkitsevyystaso 0,05 (5%), emme hylkää nollahypoteesia.
b) Koska p-arvo 0,0129 on pienempi kuin merkitsevyysaste 0,05, hylkäämme nollahypoteesin.
Esimerkki 2
27% Intian ihmisistä puhuu hindia tutkimuksen mukaan. Tutkija on utelias, onko luku korkeampi hänen kylässään. Siksi hän kehittää nolla- ja vaihtoehtoisen hypoteesin. Hän testaa H 0: p = 0,27. Ha : p> 0,27. Tässä p on kylässä hindia puhuvien ihmisten osuus. Hän teettää kyselyn kylässään selvittääkseen, kuinka moni ihminen voi puhua hindia. Hänen mukaansa 80 otokseen otetusta 240 ihmisestä voi puhua hindia. Selvitä arvioitu p-arvo tutkijan testille, jos oletamme, että tarvittavat ehdot täyttyvät ja merkitsevyystaso on 5%.
Ratkaisu:
Käytä seuraavia tietoja P-arvon laskemiseen.

Tässä näytekoko n = 240,
p 0 on väestöosuus. Meidän on löydettävä otososuus
= 80/240
 = 0,33
= 0,33
Z Tilastotiedot
Z-tilastojen laskeminen


= 0,33 - 0,27 / √ 0,27 * (1 - 0,27) / 240
Z Tilastotiedot ovat -

Z = 2,093696
P-arvo on -

P-arvo = P (z ≥ 2,09)
Meidän on tarkasteltava arvoa 2,09 on z-taulukko. Joten meidän on tarkasteltava arvoa -2,0 z-sarakkeessa ja arvoa 0,09-sarakkeessa. Koska normaali jakauma on symmetrinen, käyrän oikealla puolella oleva alue on yhtä suuri kuin vasemmalla. Saamme p-arvoksi 0,0183.
P-arvo = 0,0183
Koska p-arvo on alle merkittävän tason 0,05 (5%), hylkäämme nollahypoteesin.
Huomaa: Excelissä p-arvo on tulossa 0,0181
Esimerkki 3
Tutkimukset osoittavat, että miehet ostavat enemmän lentolippuja kuin naiset. Urokset ja naiset ostavat niitä suhteessa 2: 1. Tutkimus tehtiin tietyllä Intian lentokentällä lentolippujen jakautumisen löytämiseksi miehille ja naisille. 150 lipusta 88 miestä ostivat miehet ja 62 naiset. Meidän on selvitettävä, aiheuttaako kokeellinen manipulointi muutoksen tuloksissa, vai havaitsemmeko sattuman vaihtelua. Laske p-arvo olettaen, että merkitsevyysaste on 0,05.
Ratkaisu:
Käytä seuraavia tietoja P-arvon laskemiseen.

Vaihe 1: Havaittu arvo on 88 miehillä ja 62 naisilla.
- Odotettu arvo miehille = 2/3 * 150 = 100 miestä
- Odotettu arvo naisille = 1/3 * 150 = 50 naista
Vaihe 2: Selvitä chi-neliö


= ((88-100) 2) / 100 + (62-50) 2/50
= 1,44 + 2,88
Chi-neliö (X ^ 2)
Chi-neliö (X ^ 2) on -

Chi-neliö (X ^ 2) = 4,32
Vaihe 3: Etsi vapauden asteet
Koska muuttujia on 2 - miehet ja naiset, n = 2
Vapausasteet = n-1 = 2-1 =
Vaihe 4: P-arvotaulukosta tarkastellaan taulukon ensimmäistä riviä, koska vapausaste on 1. Voimme nähdä, että p-arvo on välillä 0,025 - 0,05. Koska p-arvo on pienempi kuin merkitsevyysaste 0,05, hylkäämme nollahypoteesin.
P-arvo on -

P-arvo = 0,037666922
Huomaa: Excel antaa p-arvon suoraan kaavan avulla:
CHITEST (todellinen alue, odotettu alue)
Esimerkki 4
Tiedetään, että 60% kaupungin vaatekauppaan tulleista ihmisistä ostaa jotain. Vaatekaupan omistaja halusi selvittää, onko hänen omistamallaan vaatekaupalla numero suurempi. Hänellä oli jo kaupalleen tehdyn tutkimuksen tulokset. Hänen kauppaansa tulleista 200 ihmisestä 128 osti jotain. Kaupan omistaja merkitsi passi niiden ihmisten osuutta, jotka tulivat hänen vaatekauppaansa ja ostivat jotain. Hänen tekemänsä nullhypoteesi oli p = 0,60 ja vaihtoehtoinen hypoteesi oli p> 0,60. Etsi tutkimuksen p-arvo merkitsevyystasolla 5%.
Ratkaisu:
Käytä seuraavia tietoja P-arvon laskemiseen.

Tässä otoskoko n = 200. Meidän on löydettävä otososuus
= 128/200
 = 0,64
= 0,64
Z Tilastotiedot
Z-tilastojen laskeminen


= 0,64 - 0,60 / √ 0,60 * (1 - 0,60) / 200
Z Tilastotiedot ovat -

Z Tilasto = 1,1547
P-arvo = P (z ≥ 1,1547)
NORMSDIST-toiminto Excelissä

NORMSDIST tulee olemaan -

NORMSDIST = 0,875893461
On sisäänrakennettu toiminto p-arvon laskemiseksi ats-tilastosta Excelissä. Se tunnetaan nimellä NORMSDIST-toiminto. Excel NORMSDIST -funktio laskee normaalin normaalin kumulatiivisen jakelutoiminnon toimitetusta arvosta. Sen muoto on NORMSDIST (z). Koska z-tilastollinen arvo on solussa B2, käytetty funktio on = NORMSDIST (B2).
P-arvo on -

P-arvo = 0,12410654
Koska meidän on löydettävä alue käyrän oikealta puolelta,
p-arvo = 1 - 0,875893 = 0,1224107
Koska p-arvo 0,1224107 on enemmän kuin merkittävä taso 0,05, emme hylkää nollahypoteesia.
Osuvuus ja käyttö
P-arvolla on laajat sovellukset tilastollisten hypoteesien testauksessa, erityisesti nollahypoteesien testauksessa. Esimerkiksi rahastonhoitaja hoitaa sijoitusrahastoa. Hän väittää, että sijoitusrahaston tietyn järjestelmän tuotot vastaavat Niftyä, joka on vertailuindeksi osakemarkkinaindeksi. Hän kehittäisi nullhypoteesin, jonka mukaan sijoitusrahastojärjestelmän tuotot vastaavat Niftyn tuottoa. Vaihtoehtoinen hypoteesi olisi, että järjestelmän tuotot ja Nifty-tuotot eivät ole samanarvoisia. Sitten hän laskee p-arvon.

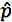 on näytteen osuus
on näytteen osuus