Kestokaava (määritelmä, Excel-esimerkkejä) | Laske joukkovelkakirjan kesto
Mikä on Duration Formula?
Duraation kaava on mitoitus joukkovelkakirjan herkkyydestä koron muutoksille, ja se lasketaan jakamalla joukkolainan diskontattujen tulevien kassavirtojen summa ja vastaava vuosimäärä diskontatun tulevan kassavirran summalla. Rahavirta koostuu periaatteessa kuponkimaksusta ja maturiteetista lopussa. Se tunnetaan myös nimellä Macaulay kesto.
Matemaattisesti keston yhtälö on esitetty alla,

missä,
- C = kuponkimaksu jaksoa kohti
- M = Kasvo- tai Par-arvo
- r = efektiivinen jaksollinen korko
- n = erääntymisaikojen lukumäärä
Lisäksi nimittäjä, joka on joukkolainan diskontatun kassavirran summa, vastaa joukkovelkakirjan nykyarvoa tai hintaa. Siksi keston kaavaa voidaan edelleen yksinkertaistaa seuraavasti:

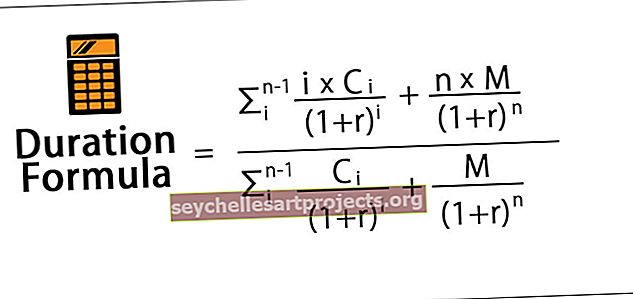
Kestokaavan selitys
Kestoyhtälö voidaan laskea käyttämällä seuraavia vaiheita:
Vaihe 1: Ensinnäkin selvitetään joukkovelkakirjan liikkeeseenlaskun nimellisarvo tai nimellisarvo ja se merkitään M.
Vaihe 2: Lainan kuponkimaksu lasketaan nyt korkojen efektiivisen jaksollisen koron perusteella. Sitten määritetään myös kuponkimaksun tiheys. Kuponkimaksu on merkitty C: llä ja efektiivinen jaksollinen korko on merkitty r: llä.
Vaihe 3: Nyt erääntymisaikojen kokonaismäärä lasketaan kertomalla erääntymisvuosien lukumäärä ja kuponkimaksujen tiheys vuodessa. Erääntymisaikojen lukumäärä on merkitty n: llä. Merkitään myös jaksoittaisen maksun aika, jota merkitään i.
Vaihe 4: Lopuksi käytettävissä olevien tietojen perusteella keston yhtälö voidaan johtaa seuraavasti:

Esimerkkejä kestokaavasta (Excel-mallin kanssa)
Katsotaanpa joitain yksinkertaisia tai edistyneitä kestokaavoja ymmärtämään sitä paremmin.
Voit ladata tämän Duration Formula Excel -mallin täältä - Duration Formula Excel -malli
Kestokaavan kaava - Esimerkki 1
Otetaan esimerkki joukkolainasta, jolla on vuotuiset kuponkimaksut. Oletetaan, että yritys XYZ Ltd on laskenut liikkeeseen joukkovelkakirjalainan, jonka nimellisarvo on 100 000 dollaria ja jonka vuotuinen kuponkikorko on 7% ja erääntyvä 5 vuodessa. Hallitseva markkinakorko on 10% .
M = 100 000 dollaria
- C = 7% * 100 000 dollaria = 7 000 dollaria
- n = 5
- r = 10%
Lainan nimittäjä tai hinta lasketaan kaavalla

- Joukkovelkakirjalainan hinta = 84281,19
Kesto-kaavan osoittaja lasketaan seuraavasti -

= (6 363,64 + 11570,25 + 15777,61 + 19124,38 + 310460,70)
= 363 296,50
Siksi joukkovelkakirjan kesto lasketaan seuraavasti:

Kesto = 363 296,50 / 84 281,19
- Kesto = 4,31 vuotta
Kestokaavan kaava - esimerkki 2
Otetaan esimerkki joukkolainasta, jolla on vuotuiset kuponkimaksut. Oletetaan, että yritys XYZ Ltd on laskenut liikkeeseen joukkovelkakirjalainan, jonka nimellisarvo on 100 000 dollaria ja erääntyvä 4 vuodessa. Hallitseva markkinakorko on 10%. Laske joukkovelkakirjan kesto seuraavalle vuotuiselle kuponkikorkolle: (a) 8% (b) 6% (c) 4%
M = 100 000 dollaria
- n = 4
- r = 10%
Laskelma kuponkikorkoon 8%
Kuponkimaksu (C) = 8% * 100 000 dollaria = 8 000 dollaria
Lainan nimittäjä tai hinta lasketaan kaavalla

- Joukkovelkakirjan hinta = 88 196,16
Kesto-kaavan osoittaja lasketaan seuraavasti:

= 311 732,8
Siksi joukkovelkakirjan kesto lasketaan seuraavasti:

Kesto = 311732,81 / 88196,16
- Kesto = 3,53 vuotta
Laskelma kuponkikorkolle 6%
Kuponkimaksu (C) = 6% * 100 000 dollaria = 6000 dollaria
Lainan nimittäjä tai hinta lasketaan kaavalla

- Joukkovelkakirjalainan hinta = 83222,46
Kesto-kaavan osoittaja lasketaan seuraavasti:

= 302,100,95
Siksi joukkovelkakirjan kesto lasketaan seuraavasti:

Kesto = 302100,95 / 83222,46
- Kesto = 63 vuotta
Laskelma kuponkikorosta 4%
Kuponkimaksu = 4% * 100 000 dollaria = 4 000 dollaria
Lainan nimittäjä tai hinta lasketaan kaavalla

- Joukkovelkakirjalainan hinta = 78248,75
Kesto-kaavan osoittaja lasketaan seuraavasti:

= 292 469,09
Siksi joukkovelkakirjan kesto lasketaan seuraavasti:

Kesto kaava = 292469,09 / 78248,75
- Kesto = 3,74 vuotta
Esimerkistä voidaan nähdä, että joukkovelkakirjalainan kesto kasvaa kuponkikoron laskiessa.
Kestokaavan merkitys ja käyttö
On tärkeää ymmärtää keston käsite, koska joukkovelkakirjasijoittajat käyttävät sitä tarkastamaan joukkolainan herkkyyden korkojen muutoksille. Lainan duraatio osoittaa periaatteessa, kuinka paljon joukkovelkakirjan markkinahinta muuttuu korkotason muutoksen takia. On huomionarvoista muistaa, että korko ja joukkovelkakirjalainan hinta liikkuvat vastakkaisiin suuntiin ja sellaisenaan koron hinnan noustessa koron laskiessa ja päinvastoin.
Jos sijoittajat haluavat hyötyä korkotason laskusta, sijoittajat aikovat ostaa pidemmän joukkolainan, mikä on mahdollista matalamman kuponkimaksun ja pitkän maturiteetin joukkovelkakirjalainalle. Toisaalta sijoittajat, jotka haluavat välttää korkojen volatiliteettia, joutuvat sijoittamaan joukkovelkakirjoihin, joiden maturiteetti tai maturiteetti on matalampi ja kuponkimaksu korkeampi.