Z Testikaava tilastoissa Vaiheittainen laskenta (esimerkkejä)

Kaava Z-testin laskemiseksi tilastoissa

Z Tilastotesti viittaa hypoteesitestiin, jota käytetään määrittämään, ovatko lasketut kaksi näytekeskiarvoa erilaiset, jos standardipoikkeamat ovat käytettävissä ja näyte on suuri.

Z = (x - μ) / ơ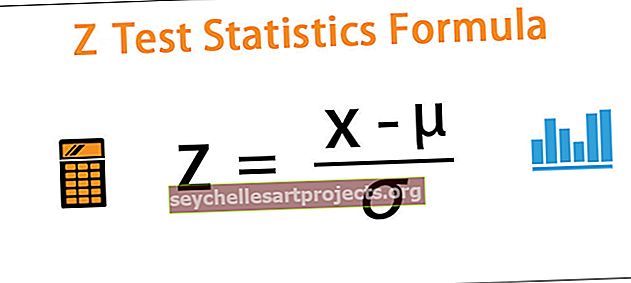

missä x = mikä tahansa populaation arvo

μ = populaation keskiarvo
population = populaation keskihajonta

Näytteen tapauksessa arvon z-testitilastojen kaava lasketaan vähentämällä otoksen keskiarvo x-arvosta ja tulos jaetaan sitten otoksen keskihajonnalla. Matemaattisesti se on esitetty

Z = (x - x_mean ) / s

missä

x = mikä tahansa arvo näytteestä
x_mean = otoksen keskiarvo
s = näytteen keskihajonta

Z Testilaskenta (vaihe vaiheelta)

Kaavan z-testitilastoille populaatiosta johdetaan käyttämällä seuraavia vaiheita:

Vaihe 1: Ensinnäkin, laskea väestön välineet ja populaation keskihajonta perustuu havaintoon jää väestön keskimääräinen, ja kukin havainto on merkitty x _i . Väestön havaintojen kokonaismäärä on merkitty N.

Väestön keskiarvo,

Väestön keskihajonta,

Vaihe 2: Lopuksi z-testitilastot lasketaan vähentämällä populaation keskiarvo muuttujasta ja tulos jaetaan sitten populaation keskihajonnalla, kuten alla on esitetty.

Z = (x - μ) / ơ

Näytteen z-testitilastojen kaava on johdettu käyttämällä seuraavia vaiheita:

Vaihe 1: Lasketaan ensin näytekeskiarvo ja näytteen keskihajonta sama kuin edellä. Tässä näytteen havaintojen kokonaismäärä on merkitty n: llä siten, että n <N.

Näytekeskiarvo,

Näyte keskihajonta,

Vaihe 2: Lopuksi z-testitilastot lasketaan vähentämällä otoksen keskiarvo x-arvosta ja tulos jaetaan sitten näytteen keskihajonnalla, kuten alla on esitetty.

Z = (x - x_mean ) / s

Esimerkkejä

Voit ladata tämän Z Test Formula Excel -mallin täältä - Z Test Formula Excel -malli

Esimerkki 1

Oletetaan, että koulussa on joukko oppilaita, jotka ilmestyivät luokkatestiin. Testin keskiarvo on 75 ja keskihajonta on 15. Määritä testissä 90 pistäneen Davidin z-testipisteet.

Koska

Populaation keskiarvo, μ = 75
Populaation keskihajonta, ơ = 15

Siksi z-testitilastot voidaan laskea seuraavasti:

Z = (90-75) / 15

Z Testitilastot ovat -

Z = 1

Siksi Daavidin testipisteet ovat yksi keskihajonta populaation keskiarvon yläpuolella, ts. Z-pistetaulukon mukaan 84,13% opiskelijoista on vähemmän pisteitä kuin David.

Esimerkki 2

Otetaan esimerkki 30 opiskelijasta, jotka valittiin tutkittavaksi otosryhmään ja selvitettiin, kuinka monta lyijykynää viikossa käytettiin. Määritä 3. opiskelijan z-testipisteet annettujen vastausten perusteella: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.

Koska

x = 5, 3. opiskelijan vastauksen jälkeen, on 5
Näytteen koko, n = 30

Näytekeskiarvo = (3 + 2 + 5 + 6 + 4 + 7 + 4 + 3 + 3 + 8 + 3 + 1 + 3 + 6 + 5 + 2 + 4 + 3 + 6 + 4 + 5 + 2 + 2 + 4 + 4 + 2 + 8 + 3 + 6 + 7) / 30

Keskiarvo = 4,17

Nyt näytteen keskihajonta voidaan laskea käyttämällä yllä olevaa kaavaa.

ơ = 1,90

Siksi 3. opiskelijan z-testipisteet voidaan laskea seuraavasti:

Z = (x - x) / s

Z = (5-17) / 1,90
Z = 0,44

Siksi 3. opiskelijan käyttö on 0,44 kertaa keskihajonta suurempi kuin otoksen keskimääräinen käyttö, ts. Z-pistetaulukon mukaan 67% opiskelijoista käyttää vähemmän lyijykyniä kuin 3. opiskelija.

Esimerkki 3

Alla on annettu tietoja Z-testitilastojen laskemiseksi

Voit käyttää alla olevaa Excel-taulukkoa Z-testitilastojen yksityiskohtaiseen laskemiseen.

Osuvuus ja käyttötarkoitukset

On erittäin tärkeää ymmärtää z-testitilastojen käsite, koska sitä käytetään yleensä aina, kun on kyseenalaista, seuraaeko testitilasto normaalijakaumaa kyseessä olevan nollahypoteesin alla vai ei. On kuitenkin pidettävä mielessä, että z-testiä käytetään vain, kun näytteen koko on yli 30, muuten käytetään t-testiä.

seychellesartprojects.org