seychellesartprojects.org

Kaava keskiarvon laskemiseksi

Keskiarvo on arvo, jota käytetään kuvaamaan datajoukkoa, samoin kuin kokonaisdatasta laskettu keskiarvo, ja tämä kaava lasketaan lisäämällä kaikki annetun joukon arvot, jotka on merkitty X: n summalla, ja jakamalla se arvojen määrällä. arvot, jotka annetaan joukossa, jota merkitään N.

Keskiarvo = (a ₁ + a ₂ +…. + A _n ) / n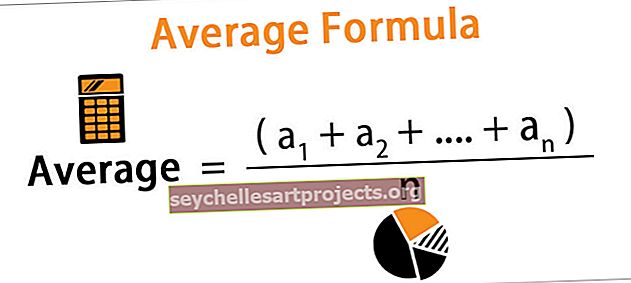

• missä a _i = havainto
• n = havaintojen lukumäärä

Selitys

Keskiarvon laskenta voidaan laskea käyttämällä seuraavia vaiheita:

• Vaihe 1: Määritä ensin havainto ja ne merkitään luvulla ₁ , ₂ , ..., a _{n, joka} vastaa 1. havaintoa, 2. havaintoa,…., N. Havaintoa.
• Vaihe 2: Määritä seuraavaksi havaintojen lukumäärä ja sitä merkitään n: llä.
• Vaihe 3: Lopuksi keskiarvo lasketaan lisäämällä kaikki havainnot ja jakamalla tulos sitten havaintojen lukumäärällä kuten alla on esitetty.

Keskiarvo = (a ₁ + a ₂ +…. + A _n ) / n

Esimerkkejä

Voit ladata tämän keskimääräisen kaavan Excel-mallin täältä - keskimääräinen kaava-Excel-malli

Esimerkki 1

Otetaanpa esimerkki Johnista, joka ilmoittautui ympäristötieteiden jatko-ohjelmaan. Kolmivuotinen tutkintokurssi on jaettu kuudeksi lukukaudeksi ja lopullinen keskimääräinen prosenttiosuus lasketaan kaikkien lukukausien pisteytettyjen prosenttiosuuksien perusteella. Laske Johnin viimeinen prosenttiosuus hänen seuraavan pistemääränsä perusteella:

Alla on annettu tietoja keskimääräisen prosenttiosuuden laskemiseksi.

Koska

a ₁ = 79%, a ₂ = 81%, a ₃ = 74%, a ₄ = 70%, a ₅ = 82%, a ₆ = 85%, n = 6

Edellä olevia tietoja käyttämällä keskiarvo lasketaan seuraavasti:

•   Keskiarvo = (79% + 81% + 74% + 70% + 82% + 85%) / 6

Keskiarvo on -

• Keskiarvo = 78,50%

Siksi David pisteytti loppuohjelman 78,5 prosentin prosenttiosuuden.

Käyttää

Kuten nimestä "keskiarvo" viittaa, se viittaa havaintojen joukon keskipisteeseen ja kun sitä käytetään matematiikan kentällä, se edustaa lukua, joka on tyypillisesti numeroryhmän keskiarvo. Termiä käytetään usein ilmaisemaan numero, joka edustaa joukkoa ihmisiä tai asioita. Se on erittäin tärkeä, koska se auttaa tiivistämään suuren määrän tietoja yhdeksi arvoksi ja osoittaa myös, että alkuperäisen datan yksittäisen arvon ympärillä on jonkin verran epäjohdonmukaisuutta, joka on erittäin tärkeä osa keskeistä suuntausteoriaa.