Väestövarianssikaava | Vaiheittainen laskenta | Esimerkkejä
Kaava väestövarianssin laskemiseksi
Populaation varianssikaava on mittari populaatiotietojen keskimääräisillä etäisyyksillä, ja se lasketaan selvittämällä populaatiokaavan keskiarvo ja varianssi lasketaan muuttujien neliön summan miinus keskiarvo summalla, joka on jaettu useilla populaatiohavainnoilla.
Väestövarianssi on väestötietojen leviämisen mittari. Siksi populaatiovarianssi voidaan määritellä keskiarvona etäisyyksistä tietystä populaatiosta jokaisesta datapisteestä keskiarvoon, neliöön ja se osoittaa kuinka datapisteet jakautuvat populaatiossa. Väestövarianssi on tärkeä tilastojen hajautumisen mittari. Tilastotieteilijät laskevat varianssin selvittääkseen, kuinka tietojoukon yksittäiset luvut liittyvät toisiinsa.
Laskettaessa populaation varianssia dispersio lasketaan populaation keskiarvon perusteella. Siksi meidän on selvitettävä populaatiokeskiarvo populaatiovarianssin laskemiseksi. Yksi suosituimmista ilmoituksista väestövarianssista on σ2. Tämä lausutaan sigma-neliöksi.
Väestön varianssi voidaan laskea käyttämällä seuraavaa kaavaa:


missä
- σ2 on populaation varianssi,
- x 1, x 2 , x 3, ... ..x n ovat havaintoja
- N on havaintojen lukumäärä,
- µ on tietojoukon keskiarvo
Väestövarianssin laskeminen askel askeleelta
Populaation varianssin kaava voidaan laskea käyttämällä seuraavia viittä yksinkertaista vaihetta:
- Vaihe 1: Laske annettujen tietojen keskiarvo (µ). Keskiarvon laskemiseksi lisää kaikki havainnot ja jaa sitten havaintojen lukumäärällä (N).
- Vaihe 2: Tee taulukko. Huomaa, että taulukon rakentaminen ei ole pakollista, mutta sen esittäminen taulukkomuodossa helpottaisi laskutoimituksia. Kirjoita ensimmäiseen sarakkeeseen kukin havainto (x 1, x 2 , x 3, ... ..x n ).
- Vaihe 3: Kirjoita toiseen sarakkeeseen kunkin havainnon poikkeama keskiarvosta (x i - µ).
- Vaihe 4: Kirjoita kolmanteen sarakkeeseen kunkin havainnon neliö keskiarvosta (x i - µ) 2. Toisin sanoen neliö kukin sarakkeessa 2 saaduista numeroista.
- Vaihe 5: Sen jälkeen meidän on lisättävä kolmannessa sarakkeessa saadut numerot. Etsi neliöpoikkeamien summa ja jaa saatu summa havaintojen määrällä (N). Tämä auttaa meitä saamaan
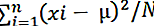 väestövarianssin.
väestövarianssin.
Esimerkkejä
Voit ladata tämän Population Variance Formula Excel -mallin täältä - Population Variance Formula Excel -malliEsimerkki 1
Laske populaation varianssi seuraavien 5 havainnon perusteella: 50, 55, 45, 60, 40.
Ratkaisu:
Käytä seuraavia tietoja populaation varianssin laskemiseen.

Havaintoja on yhteensä 5. Siksi N = 5.
µ = (50 + 55 + 45 + 60 + 40) / 5 = 250/5 = 50
Joten populaation varianssin σ2 laskeminen voidaan tehdä seuraavasti-


σ2 = 250/5
Väestövarianssi σ2 tulee olemaan-

Väestövarianssi (σ2) = 50
Väestövarianssi on 50.
Esimerkki 2
XYZ Ltd. on pieni yritys ja siinä on vain 6 työntekijää. Toimitusjohtajan mielestä näiden työntekijöiden palkoissa ei saisi olla suurta hajaantumista. Tätä varten hän haluaa sinun laskevan näiden palkkojen varianssin. Näiden työntekijöiden palkat ovat alle. Laske toimitusjohtajan palkkojen väestövaihtelu.
Ratkaisu:
Käytä seuraavia tietoja populaation varianssin laskemiseen.

Havaintoja on yhteensä 6. Siksi N = 6.
= (30 + 27 + 20 + 40 + 32 + 31) / 6 = 180/6 = 30 dollaria
Joten populaation varianssin σ2 laskeminen voidaan tehdä seuraavasti-


σ2 = 214/6
Väestövarianssi σ2 tulee olemaan-

Väestövarianssi (σ2) = 35,67
Palkkojen väestövarianssi on 35,67.
Esimerkki 3
Sweet Juice Oy valmistaa erilaisia makuja mehua. Hallinto osasto ostaa 7 isoa astiaa tämän mehun varastointiin tehtaalla. Laadunvalvontaosasto on päättänyt hylätä säiliöt, jos säiliöiden varianssi on yli 10. Annetaan 7 kontin paino kilogrammoina: 105, 100, 102, 95, 100, 98 ja 107. Ilmoita laatu Valvontaosasto siitä, pitäisikö sen hylätä säiliöt.
Ratkaisu:
Käytä seuraavia tietoja populaation varianssin laskemiseen.

Havaintoja on yhteensä 7. Siksi N = 7
= (105 + 100 + 102 + 95 + 100 + 98 + 107) / 7 = 707/7 = 10
Joten populaation varianssin σ2 laskeminen voidaan tehdä seuraavasti-


σ2 = 100/7
Väestövarianssi σ2 tulee olemaan-

Väestövarianssi (σ2) = 14,29
Koska varianssi (14,29) on yli laadunvalvontaosaston päättämän 10-arvon, säiliöt on hylättävä.
Esimerkki 4
Sagar Healthcare -nimisen sairaalan johtoryhmä kirjasi, että maaliskuun 2019 ensimmäisellä viikolla oli syntynyt 8 vauvaa. Lääkäri halusi arvioida vauvojen terveyttä ja korkeuksien vaihtelua. Näiden vauvojen korkeudet ovat seuraavat: 48 cm, 47 cm, 50 cm, 53 cm, 50 cm, 52 cm, 51 cm, 60 cm. Laske näiden 8 vauvan korkeuksien varianssi.
Ratkaisu:
Käytä seuraavia tietoja populaation varianssin laskemiseen.

Joten populaation varianssin σ2 laskeminen voidaan tehdä seuraavasti-

Excelissä on sisäänrakennettu kaava populaation varianssille, jota voidaan käyttää laskemaan joukkoryhmän populaation varianssi. Valitse tyhjä solu ja kirjoita tämä kaava = VAR.P (B2: B9). Tässä B2: B9 on solualue, jolta haluat laskea populaation varianssin.
Väestövarianssi σ2 tulee olemaan-

Populaation varianssi (σ2) = 13,98
Osuvuus ja käyttö
Populaation varianssia käytetään leviämisen mittana. Tarkastellaan kahta populaatioryhmää, joilla on sama keskiarvo ja havaintojen määrä. Tietojoukko 1 koostuu viidestä numerosta - 55, 50, 45, 50 ja 50. Tietojoukko 2 koostuu 10, 50, 85, 90 ja 15. Molemmilla tietojoukoilla on sama keskiarvo, joka on 50. Mutta tietojoukossa 1 arvot ovat lähellä toisiaan, kun taas tietojoukolla 2 on hajautettuja arvoja. Varianssi antaa tieteellisen mittauksen tästä läheisyydestä / leviämisestä. Tietojoukolla 1 on varianssi vain 10, kun taas tietojoukolla 2 on valtava varianssi 1130. Suuri varianssi osoittaa siis, että luvut ovat kaukana keskiarvosta ja toisistaan. Pieni varianssi osoittaa, että luvut ovat lähellä toisiaan.
Varianssia käytetään salkunhallinnassa omaisuuden allokoinnissa. Sijoittajat laskevat varojen tuoton vaihtelun optimaalisten salkkujen määrittämiseksi optimoimalla kaksi pääparametriä - tuotto ja volatiliteetti. Varianssilla mitattu volatiliteetti mittaa tietyn taloudellisen vakuuden riskiä.

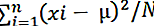 väestövarianssin.
väestövarianssin.