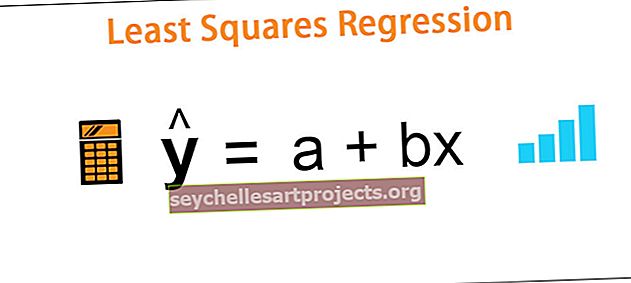seychellesartprojects.org

Vähiten neliöiden regressiomenetelmän määritelmä

Pienimmän neliösumman regressiomenetelmä on regressioanalyysin muoto, joka määrittää riippuvan ja riippumattoman muuttujan välisen suhteen lineaarisen viivan kanssa. Tätä viivaa kutsutaan "parhaiten sopivan linjaksi".

Regressioanalyysi on tilastollinen menetelmä, jonka avulla voidaan arvioida tai ennustaa yhden muuttujan tuntemattomat arvot toisen muuttujan tunnetuista arvoista. Muuttujaa, jota käytetään ennustamaan muuttujan kiinnostusta, kutsutaan riippumattomaksi tai selittäväksi muuttujaksi ja ennustettavaa muuttujaa kutsutaan riippuvaksi tai selitetyksi muuttujaksi.

Tarkastellaan kahta muuttujaa x & y. Nämä on piirretty kaavioon, jonka arvot ovat x x-akselin arvoilla y-akselilla. Nämä arvot on esitetty alla olevan kaavion pisteillä. Pisteiden läpi vedetään suora viiva, jota kutsutaan parhaiten sopivaksi viivaksi.

Pienimmän neliösumman regressiolla pyritään varmistamaan, että annettujen arvojen läpi piirretty viiva muodostaa läheisimmän suhteen arvojen välillä.

Pienimmän neliösumman regressiokaava

Regressioviiva vähiten neliöt -menetelmällä lasketaan seuraavalla kaavalla -

ŷ = a + bx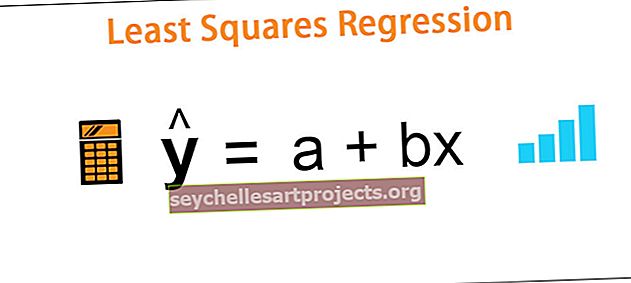

Missä,

• dependent = riippuva muuttuja
• x = riippumaton muuttuja
• a = y-leikkaus
• b = viivan kaltevuus

Viivan b kaltevuus lasketaan seuraavan kaavan avulla -

Tai

Y-leikkaus, 'a' lasketaan seuraavalla kaavalla -

Rivi parhaiten sopivaksi pienimmän neliön regressiossa

Parhaiten sopiva viiva on suora viiva, joka vedetään datapisteiden siron läpi, joka parhaiten edustaa niiden välistä suhdetta.

Tarkastellaan seuraavaa kaaviota, jossa joukko tietoja piirretään x- ja y-akseleille. Nämä datapisteet esitetään sinisillä pisteillä. Näiden pisteiden läpi piirretään kolme viivaa - vihreä, punainen ja sininen. Vihreä viiva kulkee yhden pisteen ja punainen viiva kolmen datapisteen läpi. Sininen viiva kulkee kuitenkin neljän datapisteen läpi ja jäännöspisteiden etäisyys siniseen viivaan on minimaalinen verrattuna kahteen muuhun viivaan.

Yllä olevassa kaaviossa sininen viiva edustaa parhaiten sopivaa viivaa, koska se on lähinnä kaikkia arvoja ja viivan ulkopuolella olevien pisteiden välinen etäisyys viivaan on minimaalinen (ts. Jäännösten välinen etäisyys parhaiten sopivaan viivaan - kutsutaan myös jäännösten neliösummiksi). Kahdessa muussa viivassa, oranssissa ja vihreässä, jäännösten ja viivojen välinen etäisyys on suurempi kuin sininen viiva.

Pienimmän neliösumman menetelmä tarjoaa läheisimmän suhteen riippuvien ja riippumattomien muuttujien välillä minimoimalla jäännösten ja parhaiten sopivan linjan välisen etäisyyden, ts. Jäännösten neliösummien summa on tässä lähestymistavassa minimaalinen. Tästä syystä termi "pienimmät neliöt".

Esimerkkejä pienimmän neliösumman regressioviivasta

Sovelletaan näitä kaavoja alla olevaan kysymykseen -

Voit ladata tämän pienimmän neliösumman regressio-Excel-mallin täältä - Vähiten neliöt-regressio-Excel-malli

Esimerkki 1

Yksityiskohdat teknikoiden kokemuksesta yrityksessä (useiden vuosien ajan) ja heidän suoritustasonsa on annettu alla olevassa taulukossa. Arvioi näiden arvojen avulla 20 vuoden kokemuksella varustetun teknikon suorituskyky.

Ratkaisu -

Pienimpien neliöiden laskemiseksi ensin lasketaan Y-leikkaus (a) ja viivan (b) kaltevuus seuraavasti -

Viivan (b) kaltevuus

• b = 6727 - [(80 * 648) / 8] / 1018 - [(80) 2/8]
• = 247/218
• = 1,13

Y-leikkaus (a)

• a = 648 - (1,13) (80) / 8
• = 69,7

Regressioviiva lasketaan seuraavasti -

Korvaamalla kaavan x arvo x: llä 20,

• ŷ = a + bx
• ŷ = 69,7 + (1,13) (20)
• ŷ = 92,3

20 vuoden kokemuksella varustetun teknikon suorituskyvyn arvioidaan olevan 92,3.

Esimerkki 2

Pienimmän neliösumman regressioyhtälö Excelin avulla

Pienimmän neliösumman regressioyhtälö voidaan laskea käyttämällä exceliä seuraavilla vaiheilla -

• Lisää tietotaulukko Exceliin.

• Lisää sirontakaavio datapisteiden avulla.

• Lisää trendiviiva sirontakaavioon.

• Valitse trendiviivan vaihtoehdoista - valitse lineaarinen trendiviiva ja valitse kaavion näyttöyhtälö.

• Annetun excel-tietojoukon pienimmän neliösumman regressioyhtälö näytetään kaaviossa.

Täten lasketaan pienimmän neliösumman regressioyhtälö annetulle Excel-tietojoukolle. Yhtälön avulla voidaan tehdä ennusteita ja trendianalyyseja. Excel-työkalut tarjoavat myös yksityiskohtaiset regressiolaskelmat.

Edut

• Regressioanalyysin pienimmän neliösumman menetelmä soveltuu parhaiten ennustusmalleihin ja trendianalyyseihin. Sitä käytetään parhaiten taloustieteessä, rahoituksessa ja osakemarkkinoilla, joissa minkä tahansa tulevan muuttujan arvo ennustetaan olemassa olevien muuttujien ja niiden välisen suhteen avulla.
• Pienimmän neliösumman menetelmä tarjoaa lähimmän suhteen muuttujien välillä. Jäännösneliöiden neliösumman ja parhaiten sopivan linjan välinen ero on tässä menetelmässä minimaalinen.
• Laskentamekanismi on yksinkertainen ja helppo käyttää.

Haitat

• Pienimmän neliösumman menetelmä perustuu läheisimmän suhteen luomiseen tietyn muuttujien joukon välillä. Laskentamekanismi on herkkä tiedoille, ja poikkeavien tietojen (poikkeukselliset tiedot) tapauksessa tulokset voivat yleensä vaikuttaa merkittävästi.
• Tämän tyyppinen laskenta sopii parhaiten lineaarisille malleille. Epälineaarisissa yhtälöissä käytetään tyhjentävämpiä laskentamekanismeja.

Johtopäätös

Pienimmän neliösumman menetelmä on yksi suosituimmista menetelmistä ennustusmalleissa ja trendianalyyseissä. Kun se lasketaan asianmukaisesti, se tuottaa parhaat tulokset.