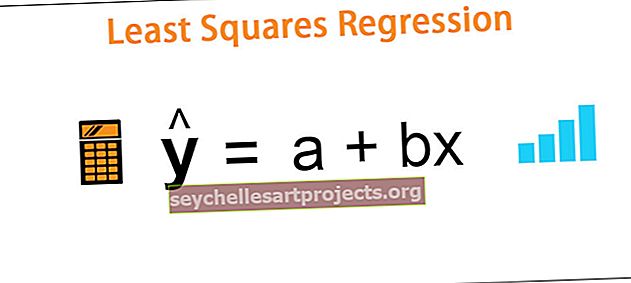LOG in Excel (kaava, esimerkkejä) | Kuinka LOG-toimintoa käytetään Excelissä?
LOG-funktiota excelissä käytetään tietyn luvun logaritmin laskemiseen, mutta saalis on, että numeron perustan antaa käyttäjän itse, se on sisäänrakennettu toiminto, johon pääsee Excelin kaava-välilehdeltä ja ottaa kaksi argumenttia, toinen on numerolle ja toinen perustalle.
LOKI Excelissä
LOG-funktio Excelissä laskee luvun logaritmin määrittelemäämme perustaksi. LOG in Excel on luokiteltu matematiikan / trigonometrian funktioksi Excelissä. LOG Excelissä palauttaa aina numeerisen arvon.
Matematiikassa logaritmi on päinvastoin kuin eksponentti. Se tarkoittaa, että minkä tahansa tietyn luvun logaritminen arvo on eksponentti, jolle perusta on nostettava, kyseisen luvun tuottamiseksi. Esimerkiksi,
25 = 32
Annetulle numerolle 32 5 on eksponentti, jolle perusta 2 on nostettu tuottamaan luku 32. Joten 32 LOG on 5.
Matemaattisesti kirjoitamme sen log 2: ksi 32 = 5, joka on LOG 32: sta tukiasemaan 2 on 5.
LOG-kaava Excelissä

Luku: on positiivinen reaaliluku (ei pitäisi olla 0), jolle haluamme laskea logaritmin Excelissä
Base: se on valinnainen argumentti, se on base, jolle logaritminen arvo lasketaan, ja LOG-funktio Excelissä oletusarvoisesti ottaa perustan arvoksi 10.
Kuinka LOG-toimintoa käytetään Excelissä?
LOG in Excel on erittäin yksinkertainen ja helppo käyttää. Anna ymmärtää LOG-toiminnon toimintaa Excelissä jollakin LOG-kaavan esimerkillä.
Voit ladata tämän LOG Function Excel -mallin täältä - LOG Function Excel -malli

Logaritmista funktiota käytetään matemaattisiin operaatioihin, ja sitä käytetään laajalti rahoitustilastoissa. Liiketoiminta-analyysissä LOG in Excel -ohjelmaa käytetään usein muiden regressioanalyysityökalujen ja kaavioiden piirtämiseen tietojen esittämiseen. Logaritmisia toimintoja käytetään graafiseen esitykseen, kun tietojen muutosnopeus kasvaa tai laskee nopeasti.
POWER-funktio palauttaa luvun, joka on korotettu tehoon, päinvastoin, LOG-toiminto Excelissä palauttaa sen voiman (eksponentin), johon perusta on nostettu.
LOG Excel-esimerkissä # 1
Esimerkiksi 45 = 1024, käyttämällä POWER-funktiota kirjoitamme sen POWER (4,5) = 1024, nyt jos pesimme tämän POWER-funktion kaavan Excelin lokitoiminnon sisälle, jolloin perusta on 4, saamme eksponentin joka välitetään POWER-funktion toisena argumenttina.

POWER-funktion lähtö välitetään ensimmäisenä argumenttina Excelin LOG-funktioon ja se laskee tuloksen edelleen.
LOGia Excelissä voidaan käyttää monin tavoin; Logaritmi auttaa ratkaisemaan reaalimaailman ongelmia. Esimerkiksi maanjäristyksen voimakkuus lasketaan muodostuneiden seismisten aaltojen amplitudin logaritmina.
Maanjäristyksen voimakkuutta edustaa LOG-kaava:
R = log 10 (A / A 0 )
Missä A on amplitudi-maanjäristysaallon mittaus ja A 0 on pienin seismisen aktiivisuuden kirjattu amplitudi, joten jos meillä on arvot A ja A 0 , voimme helposti laskea maanjäristyksen voimakkuuden Excelissä LOG-kaavalla:
= LOKI ((A / A 0 ), 10)
LOG Excel-esimerkissä # 2
Oletetaan, että meillä on näytteitä liuoksista, jotka on merkitty aakkosilla A, B, C… .L. Meille toimitetaan [H +] -ionikonsentraatio µ mol / litra Excel-taulukossa sarakkeessa B ja haluamme löytää, mikä liuos on hapan, emäksinen tai vesi. Tietotaulukko on annettu alla:

Kemiallisen liuoksen happama ja emäksinen luonne mitataan sen pH-arvolla, joka lasketaan kaavalla:
pH = -log 10 [H +]
Jos pH on alle 7, se on hapan liuos, jos pH on yli 7, se on emäksinen (emäksinen) liuos ja kun pH on 7, se on neutraali, ettei se ole hapan eikä emäksinen, kuten vesi.
Joten ratkaisun happaman ja emäksisen luonteen löytämiseksi käytämme LOGia Excelissä ja tarkistamme sen, että logaritminen arvo on pienempi, suurempi tai yhtä suuri kuin 7.
Koska annettu vetypitoisuus on yksikössä µmol / litra. Siksi arvo on X * 10-6
Joten LOG in excel löytää ratkaisun luonteen
= JOS (- (LOG (B4 * TEHO (10, -6), 10)) 7, ”Alkalinen”, ”Vesi”)) +
Lasketaan [H +] -pitoisuuden * tehon (10, -6) log- arvo, koska käytetty yksikkö on µmol / litra, ja tarkistetaan IF-funktiolla, jos arvo on suurempi, pienempi tai yhtä suuri kuin 7.
Käyttämällä kaavaa muissa soluissamme,

Tuotos:


T hän liuos leimattu I, on pH-arvo yhtä suuri kuin 7, joten se on puhdasta vettä.
LOG Excel-esimerkissä # 3
Tietojenkäsittelytieteessä jokaisen algoritmin tehokkuus mitataan sen perusteella, kuinka nopeasti se hakee tuloksen tai antaa tuloksen. Tämä hyötysuhde lasketaan teknisesti ajan monimutkaisuuden perusteella. Ajan monimutkaisuus kuvaa aikaa, jonka algoritmi suorittaa.
Joukon luettelossa olevan kohteen hakemiseksi on olemassa erilaisia algoritmeja, esimerkiksi Bubble sort, Quick sort, Merge sort, Binary Sort jne. Jokaisella algoritmilla on erilainen tehokkuus ajallisen monimutkaisuuden suhteen.
Harkitse esimerkki,
meillä on lajiteltu taulukko,

Nyt haluamme etsiä numeroa 18 annetun numeron taulukosta. Array Pointer
Tämä algoritmi noudattaa jakamis- ja sääntömenetelmää, jossa se jakaa joukon tasaisesti iteroinnin jokaisessa vaiheessa ja etsii kohdetta löydettyään kohteen, silmukat (iteraatio) lopetetaan ja palautetaan arvo.
Vaihe 1:

Vaihe 2:

Vaihe 3:

Vaihe 4:

Numero 18 löydettiin sijainnista 9, ja kohteen etsiminen binäärisen hakualgoritmin avulla vei neljä vaihetta.
Niinpä binäärihaun monimutkaisuus lasketaan log 2 N: nä, missä n on alkioiden lukumäärä
= LOG (16,2) = 4

Jos siis haluat etsiä kohdetta joukosta kohteita, binaarihaku vie lokiin 2 N vaihetta.
Oletetaan, että meille toimitetaan luettelo, joka sisältää alkioiden kokonaismäärän, ja etsimään kohteista näistä kohteista käytämme binaarihakualgoritmia. Nyt meidän on löydettävä, kuinka monta vaihetta tarvitaan kohteen löytämiseksi annetuista kohteista.

Jälleen käytämme LOGia Excelissä monimutkaisuuden laskemiseksi.
LOG-kaava on: = PYÖRÄ (LOG (A6,2), 0)
Tulos voi olla desimaalin tarkkuudella, joten olemme pyöristäneet 0 paikan tuloksen.
Yhdistämällä "Tarvittavat merkkijonot" olemme
= ”Vaaditut vaiheet ovat” & ”“ & PYÖRÄ (LOKI (A6,2), 0)

Jos haluat etsiä kohdetta, 1000000 kohteen joukosta binäärihaku vie vain 20 vaihetta.
LOG-toimintoja käytetään myös laajalti taloustieteessä osakekurssien indeksointikaavioihin, ja nämä kaaviot ovat erittäin hyödyllisiä hintojen laskun tai nousun tarkistamiseksi.